retour

Soit $f$ une fonction dérivable sur $\mathbb R$ et $\mathscr C$ sa courbe représentative.
On sait que les points \[A(-2;-1),\quad B(0,1)\quad\text{et}\quad C(2;1)\] appartiennent à $\mathscr C$.

1. Dans un repère, placer les points $A$, $B$ et $C$.
   Corrigé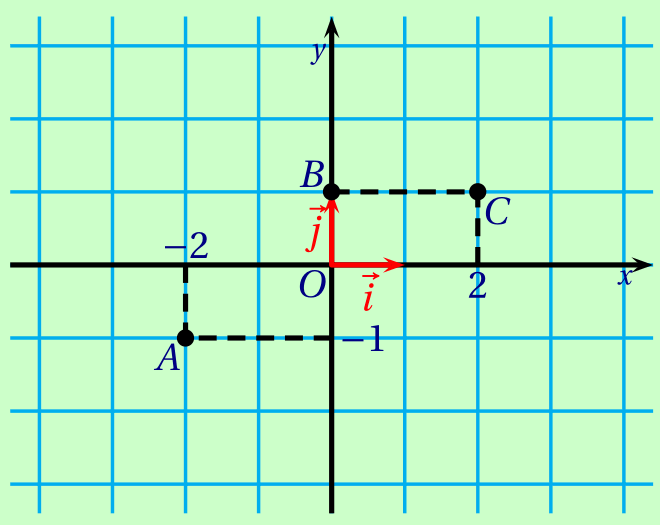
   
2. On sait de plus que \[f'(-2) = -1,\quad f'(0) = 0 \quad\text{et}\quad f'(2) = 2.\] Tracer les tangentes à $\mathscr C$ en $A$, $B$ et $C$.
   Corrigé
   La tangente en $A$ a pour coefficient directeur $f'(-2)=-1$.
   La tangente en $B$ a pour c.d. $0$.
   La tangente en $C$ a pour c.d. $2$.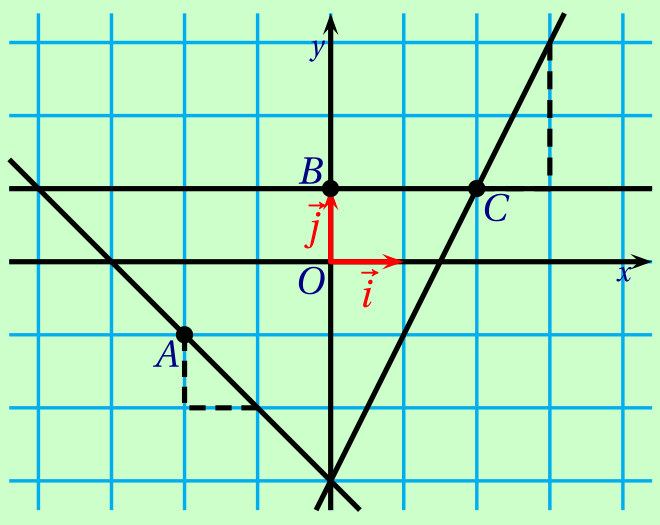

   
3. Dessiner une courbe pouvant représenter $\mathscr C$.
   Corrigé
   Une courbe possible pour $f$ (les tangentes doivent «coller» à la courbe autours du point)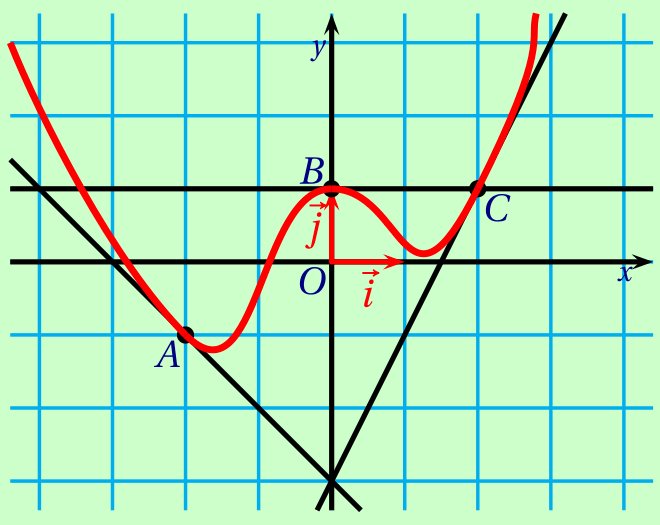

   

retour

code : 763