retour

Soit $g$ la fonction définie sur ℝ par \[g(x) = x^2\mathrm e^x.\]

1. Étudier les variations de la fonction $g$.
   Corrigé
   La fonction $g$ est dérivable sur ℝ et \[\forall x\in\mathbb R,\qquad g'(x) = 2x\mathrm e^x + x^2\mathrm e^x = (x^2 + 2x)\mathrm e^x.\] Puisque \[\mathrm e^x>0,\] $g'(x)$ est du signe du polynôme de degré 2: \[x^2 + 2x.\] Ses racines évidentes sont −2 et 0 et son coefficient principal est 1, donc positif.
   On en déduit le signe de $f'$ et les variations de $f$: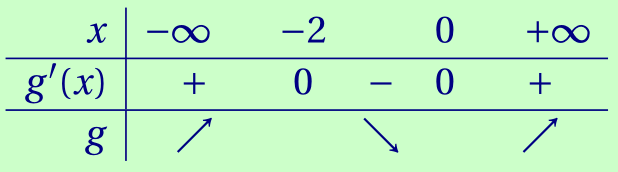

   
2. Étudier la convexité de la fonction $g$.
   Corrigé
   $g'$ est aussi dérivable sur ℝ et pour tout réel $x$: \[ g''(x) = (2x+2)\mathrm e^x + (x^2 + 2x)\mathrm e^x = (x^2 + 4x + 2)\mathrm e^x. \] Puisque l'exponentielle est strictement positive, $g''(x)$ est du signe du polynôme de degré 2 \[x^2 + 4x + 2.\] Son discriminant est $\Delta = 4^2 - 4\times 1 \times 2 = 8$.
   Il est strictement positif, donc le polynôme admet les racines \[\begin{aligned} x_1 &= \frac{-4 - \sqrt{8}}{2\times 1} = \frac{-4 -2\sqrt{2}} 2 = \frac{2(-2-\sqrt 2)}2& \\ &= -2-\sqrt 2;& \\ x_2&= \frac{-4 + \sqrt{8}}{2\times 1} = \frac{-4 +2\sqrt{2}} 2 = \frac{2(-2+\sqrt 2)}2& \\ &= -2+\sqrt 2;& \end{aligned}\] Le coefficient principal de ce polynôme est 1, donc il est positif.
   On en déduit le signe de $g''$, donc la convexité de $g$:

   

   Remarque. La courbe de $g$ admet deux points d'inflexions, d'abscisses $-2-\sqrt 2$ et $-2+\sqrt 2$.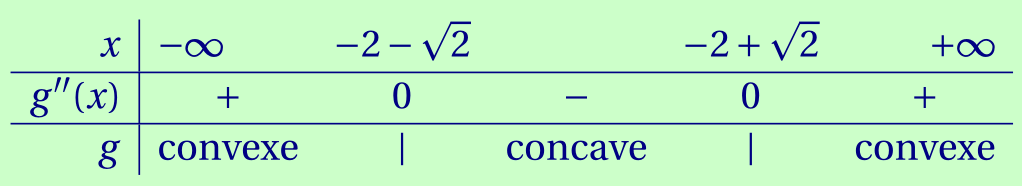

retour

code : 760