retour

Soit $f$ la fonction deux fois dérivable sur ℝ définie par : \[f(x) =x^3 - \dfrac 3 2 x^2 - \dfrac 1 2.\]

1. Étudier les variations de la fonction $f$.
   Corrigé
   La fonction $f$ est dérivable sur ℝ et \[\forall x\in\mathbb R,\qquad f'(x) = 3x^2 - \frac 3 2 \cdot 2x = 3x^2 - 3x.\] C'est un polynôme de degré 2, dont les racines évidentes sont $0$ et $1$, de coefficient principal $3$ positif.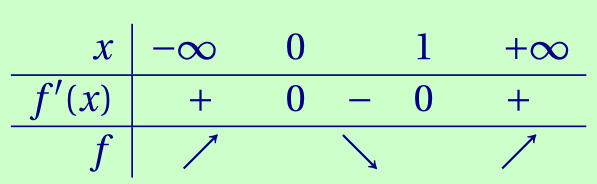

   
2. Étudier la convexité de la fonction $f$.
   Corrigé
   La fonction $f'$ est aussi dérivable sur ℝ et \[\forall x\in\mathbb R,\qquad f''(x) = 3\cdot 2x - 3 = 6x - 3.\] C'est une fonction affine, de coefficient directeur positif, qui s'annule en 2.

   

   Remarque. Le point d'abscisse 2 est l'unique point d'inflexion de la courbe de $f$.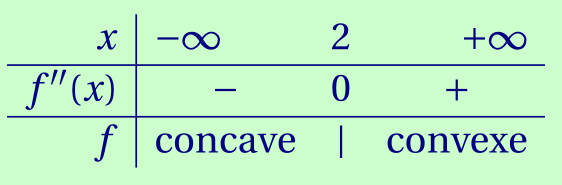
3. Donner l'équation de la tangente à la courbe de $f$ au point d'abscisse 2.
   Corrigé
   On a : \[f(2) = 2^3 - \frac 3 2 \cdot 2^2 - \frac 1 2 = \frac 3 2\] et \[f'(2) = 3\times 2^2 - 3\times 2 = 6.\] Donc l'équation de la tangente au point d'abscisse 2 est \[\begin{aligned} y &= f'(2)(x-2) + f(2)& \\ \iff y &= 6(x-2)+\frac 3 2& \\ \iff y &= 6x - \frac{21} 2.& \end{aligned}\]

retour

code : 759