EX-36
retour
On considère la fonction $f$ dérivable sur $\mathbb R$ telle que \[f(x) = (-x^2+3x-1)\mathrm e^{-x}.\]
-
Déterminer une expression de la dérivée de $f$.
CorrigéPour tout réel $x$: \[\begin{aligned} f'(x) &= (-2x+3)\mathrm e^{-x} + (-x^2+3x-1)(-\mathrm e^{-x})&\\ &=-2x\mathrm e^{-x} + 3\mathrm e^{-x} + x^2\mathrm e^{-x}-3x\mathrm e^{-x}+\mathrm e^{-x}&\\ &=(-2x+3+x^2-3x+1)\mathrm e^{-x}&\\ &=(x^2-5x+4)\mathrm e^{-x}.& \end{aligned}\]
-
Donner le tableau de signe de cette dérivée sur $\mathbb R$.
CorrigéPuisque, pour tout réel $x$, $\mathrm e^x > 0$, $f'(x)$ est du signe du polynôme \[x^2 - 5x + 4 = 0.\] Il admet la racine évidente $1$, et comme le produit des racines est $4$, l'autre racine est $4$.
Son coefficient principal est positif, il est donc positif à l'extérieur de ses racines.
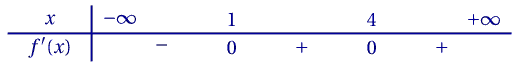
-
En déduire les variations de $f$ sur $\mathbb R$.
CorrigéLa fonction $f$ est donc décroissante sur $]-\infty;1]$ puis croissante sur $[1;4]$ puis décroissante sur $[4;+\infty[$.
-
Donner une équation de la tangente à la courbe représentative de $f$ au point d'abscisse $-2$.
CorrigéSachant que: \[\begin{aligned} f(a) = f(-2) &=\left(-(-2)^2+ 3(-2) -1\right)\mathrm e^{-(-2)}&\\ &=(-4-6-1)\mathrm e^2&\\ &=-11\mathrm e^2&\\ f'(a) = f'(-2) &=\left((-2)^2 - 5(-2) + 4\right)\mathrm e^{-(-2)}&\\ & = (4+10+4)\mathrm e^2&\\ & = 18\mathrm e^2& \end{aligned}\] l'équation de la tangente est: \[\begin{aligned} &y = f'(a)(x-a) + f(a)&\\ \iff &y = 18\mathrm e^2(x+2) - 11\mathrm e^2&\\ \iff &y = 18\mathrm e^2x + 36\mathrm e^2 - 11\mathrm e^2&\\ \iff &y = 18\mathrm e^2x + 25\mathrm e^2.& \end{aligned}\]
retour
code : 702