6.05
retour
Une voiture achetée 21 000€ le 1ier janvier 2020 perd 11% de sa valeur par an.
En quelle année vaudra-t-elle moins de 7 000€ ?
Début corrigé
fin (méthode heuristique)
fin (résolution d'inéquation)
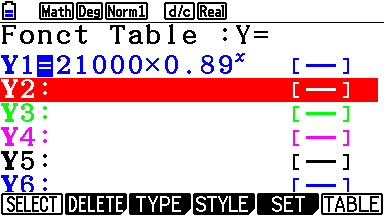
Chaque année, le prix de la voiture est multiplié par
\[1 - \frac{11}{100} = 0,89.\]
Donc son prix, au bout de $n$ années, est :
\[p(n) = 21000\times 0,89^n.\]
On souhaite donc déterminer $n$ tel que
\[21000 \times 0,89^n < 7000.\]
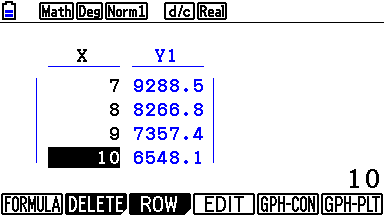
On mène une recherche à l'aide de la calculatrice. On constate que
\begin{align*}
p(9)&\approx 7357&
\\
p(10)&\approx 6548.&
\end{align*}
Il faudra donc attendre l'année 2020+10=2030.


\[\begin{aligned}
21000 \times 0,89^n &< 7000&
\\ \iff
0,89^n &< \frac{7000}{21000}&
\\ \iff
0,89^n &< \frac 1 3&
\\ \iff
\ln\left(0,89^n\right) &< \ln\left(\frac 1 3\right)&
\\ \iff
n\ln(0,89) &< -\ln(3)&
\\ \iff
n &> -\frac{\ln(3)}{\ln(0,89)}.&
\end{aligned}\]
Or
$-\dfrac{\ln(3)}{\ln(0,89)} \approx 9,427$.
Donc il faudra attendre l'année $2020+10=2030$.

retour
code : 70