retour

$f$ est une fonction définie et dérivable sur $\mathbb R$.
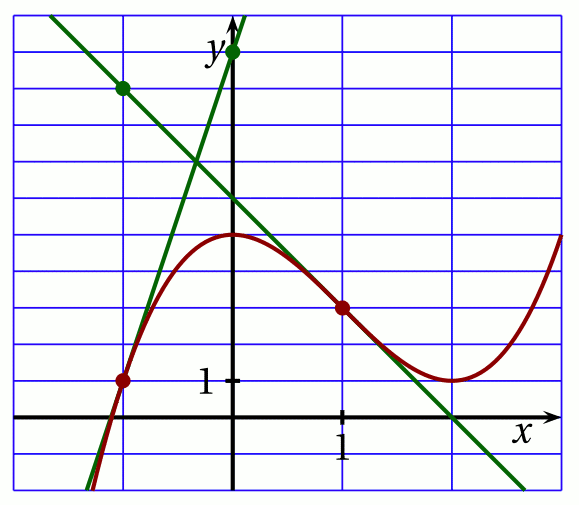
Sa courbe représentative $\mathscr C_f$ ainsi que les tangentes à $\mathscr C_f$ aux points d'abscisses $-1$ et $1$ sont tracées ci-dessous.

$g$, $h$ et $k$ sont les fonctions définies sur $\mathbb R$ par: \[g(x) = f(-x),\ h(x) = f(2x)\ \text{et}\ k(x) = f(x-2).\]

1. Lire sur le graphique :
   • $f'(-1)$ ; Corrigé
     Par lecture du coefficient directeur de la tangente : \[f'(-1) =\frac{10-1}{1-0} = 9.\]
   • $f'(1)$. Corrigé
     Par lecture du coefficient directeur de la tangente : \[f'(1) = \frac{3 - 9}{1-(-1)} =\frac 6 {-2} = -3.\]
2. En déduire :
   • $g'(-1)$, Corrigé
     $g(x) = f(ax+b)$ avec $a=-1$ et $b=0$, donc \[g'(x) = af'(ax+b) = -f'(-x).\] Alors : \[ g'(-1) = -f'(-(-1)) = -f(1) = -(-3) = 3. \]
   • $g'(1)$, Corrigé
     On a vu à la question précédente que : \[g'(x) = af'(ax+b) = -f'(-x).\] Alors : \[g'(1) = -f'(-1) = -9.\]
   • $h'(0,5)$, Corrigé
     $h(x) =f(ax+b)$ avec $a=2$ et $b=0$, donc \[h'(x) = af'(ax+b) = 2f'(2x).\] Alors : \[ \begin{aligned} h'(0,5) &= 2f'(2\times 0,5)& \\ &= 2f'(1)& \\ &= 2\times(-3)& \\ &= -6.& \end{aligned} \]
   • $k'(1)$. Corrigé
     $k(x) = f(ax+b)$ avec $a=1$ et $b=-2$, donc \[k'(x) = af'(ax+b) = f'(x-2).\] Alors \[k'(1) = f'(1-2) = f'(-1) = 9.\]

retour

code : 679