EX-17
retour
On a représenté ci-dessous les courbes $\mathscr C_f$, $\mathscr C_g$ et $\mathscr C_h$ de trois fonctions $f$, $g$ et $h$ définies et dérivables sur $\mathbb R$.
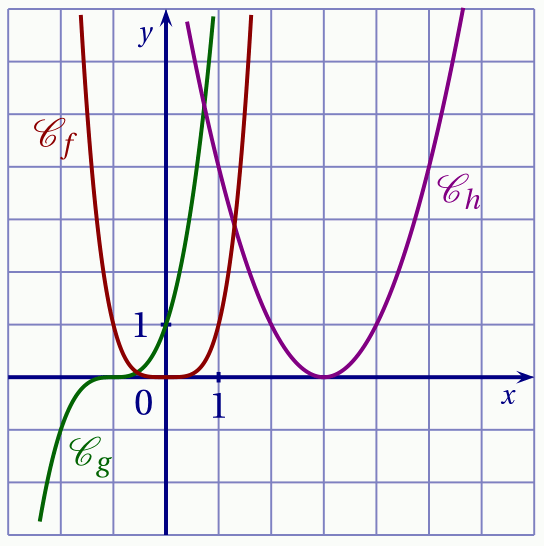
On a aussi représenté ci-dessous les courbes $\mathscr D_1$, $\mathscr D_2$ et $\mathscr D_3$ des fonctions dérivées de $f$, $g$ et $h$ (pas nécessairement dans cet ordre).
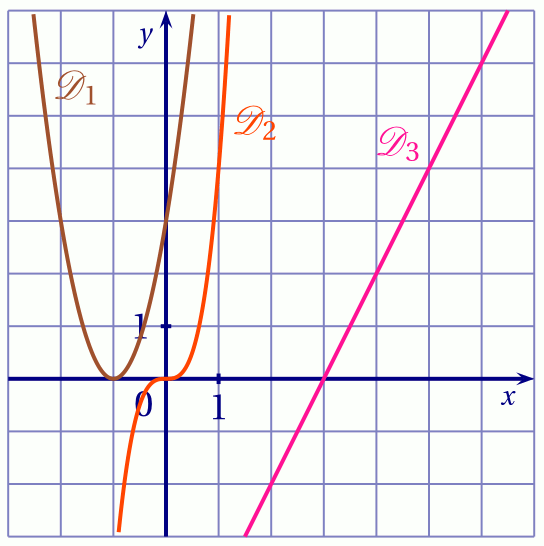
En justifiant la réponse, associer chaque courbe de fonction à la courbe de sa fonction dérivée.
Corrigé
-
La fonction $f$ est décroissante sur $]-\infty;0]$ et croissante sur $[0;+\infty[$.
Sa dérivée est donc négative sur $]-\infty;0]$ et positive sur $[0;+\infty[$.
Elle est donc représentée par la courbe $\mathscr D_2$. -
La fonction $g$ est croissante sur $\mathbb R$.
Sa dérivée est donc positive sur $\mathbb R$.
Sa courbe est donc $\mathscr D_1$. -
La fonction $h$ est décroissante sur $]-\infty;3]$ puis croissante sur $[3;+\infty[$.
Sa dérivée est donc négative sur $]-\infty;3]$ puis positive sur $[3;+\infty[$.
Elle est donc représentée par $\mathscr D_3$.
retour
code : 677