retour

On considère la fonction $f$ dérivable sur $[-2;10]$ dont la fonction dérivée $f'$ admet le tableau de signes ci-dessous.

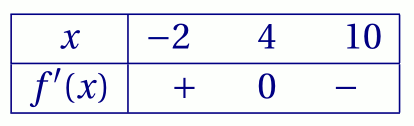
Justifier chacune des affirmations suivantes :

1. $f(5)\geqslant f(8)$;
   Corrigé
   D'après le tableau de signe, $f'$ est négative sur $[5;8]$, donc $f$ est décroissante sur cet intervalle.
   Alors \[5 \leqslant 8 \implies f(5) \geqslant f(8).\]
2. $f(0)\le f(3)$;
   Corrigé
   $f'$ est positive sur $[0;3]$, donc $f$ est croissante sur cet intervalle.
   Donc \[0 \leqslant 3 \implies f(0)\leqslant f(3).\]
3. $f$ admet un maximum en $x=4$.
   Corrigé
   D'après le tableau de signe de $f'$, $f$ est décroissante sur $[-2;4]$ puis croissante sur $[4;10]$.
   Elle admet donc bien un minimum en $x=4$.

retour

code : 676