retour

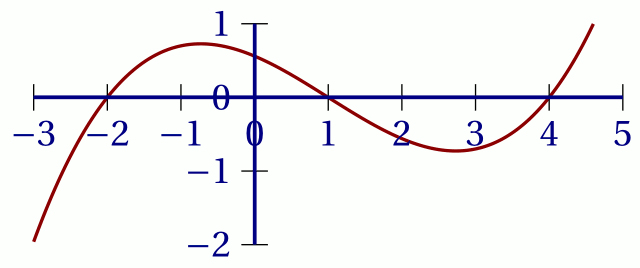
Soit $f$ une fonction définie et dérivable sur $[-3;5]$ dont la fonction dérivée $f'$ est représentée ci-dessous.

1. Dresser le tableau de signe de $f'(x)$ sur $[-3;5]$.
   Corrigé
   Tableau de signe de $f'(x)$:
   
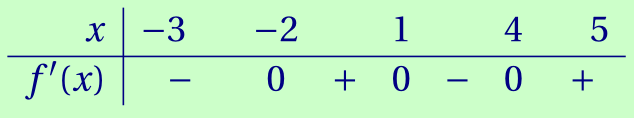
2. En déduire les variations de $f$ sur $[-3;5]$.
   Corrigé
   La fonction $f$ est donc décroissante sur $[-3;-2]$, croissante sur $[-2;-1]$, décroissante sur $[-1;4]$ et croissante sur $[4;5]$.

retour

code : 675