retour

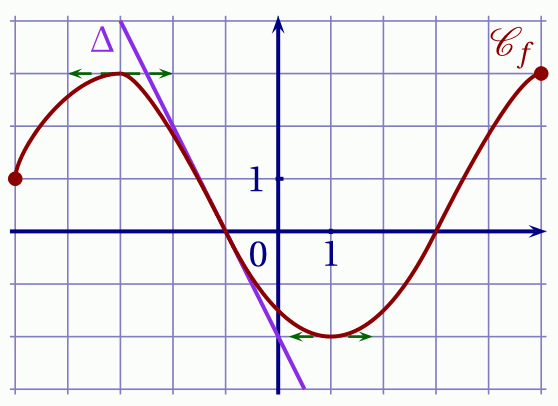
Soit $f$ la fonction définie sur $[-5;5]$ dont la représentation graphique $\mathscr C_f$ est donnée ci-dessous.

1. Résoudre graphiquement l'inéquation $f(x) \le 0$.
   Corrigé
   Les points de $\mathscr C_f$ situés sous l'axe des abscisses ont des abscisses comprises entre $-1$ et $3$.
   Donc l'inéquation $f(x)\leqslant 0$ a pour ensemble solution \[S = [-1\;;\;3].\]
2. Résoudre graphiquement l'inéquation $f'(x) \le 0$.
   Corrigé
   $f'(x) \le 0$ si et seulement si $x$ appartient à un intervalle sur lequel $f$ est décroissante.
   Donc l'inéquation $f'(x)\leqslant 0$ a pour ensemble solution \[S = [-3\;;\;1].\]
3. La droite $\Delta$ est tangente à $\mathscr C_f$ au point d'abscisse $-1$. Déterminer graphiquement $f'(-1)$.
   Corrigé
   Déterminons le coefficient directeur de la droite $\Delta$.
   Elle passe par les points de coordonnées $(-2;2)$ et $(0;-2)$ donc ce coefficient directeur est : \[\frac{-2 - 2}{0 - (-2)} = \frac{-4}{2} = -2.\] Puisque $\Delta$ est tangente à la courbe au point d'abscisse $-1$, ce coefficient directeur est aussi le nombre dérivé de $f$ en $-1$ : \[f'(-1) = -2.\]

retour

code : 660