retour

On considère le cube $ABCDEFGH$ de côté 5 ci-dessous.

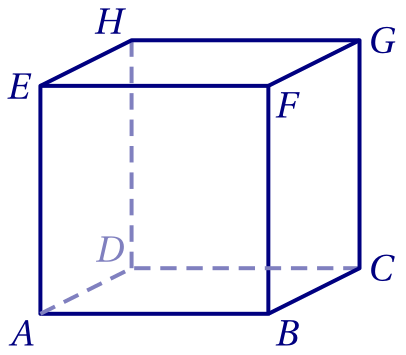
Calculer les produits scalaires suivants :

1. $\overrightarrow{BA}\cdot\overrightarrow{BC}$;     Corrigé
   $\overrightarrow{BA}\cdot\overrightarrow{BC} = 0 \Leftarrow \overrightarrow{BA}\perp\overrightarrow{BC}$.
2. $\overrightarrow{AE}\cdot\overrightarrow{DC}$;     Corrigé
   $\overrightarrow{AE}\cdot\overrightarrow{DC} = 0 \Leftarrow \overrightarrow{AE}\perp\overrightarrow{BD}$.
3. $\overrightarrow{AD}\cdot\overrightarrow{AC}$;     Corrigé
   $C$ se projette orthogonalement sur $(AD)$ en $D$, donc:
   $\overrightarrow{AD}\cdot\overrightarrow{AC} = (\overrightarrow{AD})^2 = AD^2 = 5^2 = 25$.
4. $\overrightarrow{BF}\cdot\overrightarrow{CG}$;     Corrigé
   $\overrightarrow{BF}=\overrightarrow{CG}$ donc:
   $\overrightarrow{BF}\cdot\overrightarrow{CG} = (\overrightarrow{BF})^2 = BF^2 = 5^2 = 25$.
5. $\overrightarrow{EH}\cdot\overrightarrow{BC}$;     Corrigé
   $\overrightarrow{EH} = \overrightarrow{BC}$ donc:
   $\overrightarrow{EH}\cdot\overrightarrow{BC} = (\overrightarrow{EH})^2 = EH^2 = 5^2 = 25$.
6. $\overrightarrow{AB}\cdot\overrightarrow{EG}$.     Corrigé
   $\overrightarrow{EG}=\overrightarrow{AC}$ et $C$ se projette orthogonalement sur $(AB)$ en $B$ donc:
   $\overrightarrow{AB}\cdot\overrightarrow{EG} = \overrightarrow{AB}\cdot\overrightarrow{AC} =(\overrightarrow{AB})^2 = AB^2 = 5^2 = 25$.

retour

code : 618