7.07

retour

Pour tout entier naturel $n$, on considère la fonction $f_{n}$ définie sur $]0;+\infty[$ par : \[f_{n}(x) = - nx - x \ln x.\] On note $\left(\mathcal{C}_{n}\right)$ la courbe représentative de la fonction $f_{n}$, dans un repère orthonormé $(O;\vec i,\vec j)$.

Les courbes $\left(\mathcal{C}_{0}\right)$, $\left(\mathcal{C}_{1}\right)$ et $\left(\mathcal{C}_{2}\right)$ représentatives des fonctions $f_{0}$, $f_{1}$ et $f_{2}$ sont données ci-dessous.

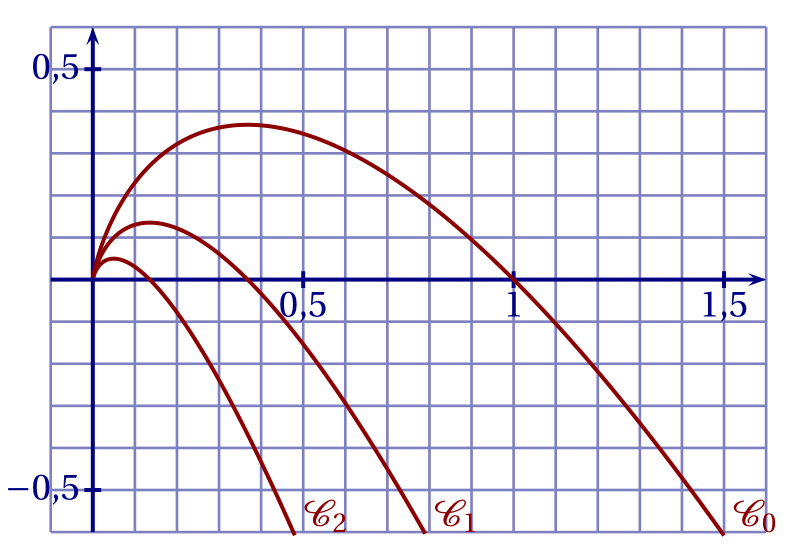
courbes de fonctions

On rappelle que $\displaystyle\lim_{x \to 0} x \ln x = 0$.

Partie A : Étude de la fonction $f_{0}$

La fonction $f_0$ est définie sur $]0;+\infty[$ par \[f_{0}(x) = -x\ln x.\]

1 Déterminer la limite de $f_{0}$ en $+\infty$.
Corrigé

Puisque \[\displaystyle\lim_{x\to +\infty} -x = -\infty \] et \[\displaystyle\lim_{x\to+\infty} \ln x = +\infty,\] on a par produit de limites : \[\lim_{x\to+\infty} -x\ln x = -\infty.\]

2 Étudier les variations de la fonction $f_{0}$ sur $]0;+\infty[$.
Corrigé

$f_0$ est le produit de deux fonctions dérivables sur $]0;+\infty[$, donc dérivable sur cet intervalle. \[f_0'(x) = -1\ln x -x\times\frac 1 x = -\ln x - 1.\] Or: \[\begin{aligned} f_0'(x) &= 0& \\ \iff -\ln x - 1 &= 0& \\ \iff \ln x&= -1& \\ \iff x &= \mathrm e^{-1}& \\ \iff x &=\frac 1 {\mathrm e} \end{aligned}\] et \[\begin{aligned} f_0'(x) > 0 \\ \iff -\ln x - 1 > 0 \\ \iff \ln x <-1 \\ \iff x <\mathrm e^{-1} \\ \iff x <\frac 1 {\mathrm e} \end{aligned}\] Donc $f_0$ est strictement croissante sur $]0;\frac 1 {\mathrm e}]$ puis strictement décroissante sur $[\frac 1 {\mathrm e};+\infty[$.

Partie B : Étude de certaines propriétés de la fonction $f_{n}$

Soit $n$ un entier naturel.

1. Démontrer que pour $x \in ]0;+\infty[$, \[f'_{n}(x) = -n -1 -\ln x\] où $f'_{n}$ désigne la fonction dérivée de $f_{n}$.
Corrigé

$f'_n$ est le produit de deux fonctions dérivables sur $]0;+\infty[$, donc dérivable sur cet intervalle : \[\begin{aligned} f'_n(x) &= -n\times 1 - 1\ln x - x\times \frac 1 x& \\ &= -n -\ln x -1& \\ &= -n - 1 - \ln x.& \end{aligned}\]

2.a. Démontrer que la courbe $\left(\mathcal{C}_{n}\right)$ admet en un unique point $A_{n}$ d'abscisse $\mathrm{e}^{-n-1}$ une tangente parallèle à l'axe des abscisses.
Corrigé

La courbe $(\mathcal C_n)$ admet une tangente horizontale en un point d'abscisse $x$ si et seulement si $f'_n(x) = 0$.
Or : \[\begin{aligned} f'_n(x) &= 0& \\ \iff -n - 1 -\ln x &= 0& \\ \iff \ln x &= - n - 1& \\ \iff x &= \mathrm e^{-n -1}.& \end{aligned}\] Le seul point de la courbe en lequel la tangente est horizontale a bien pour abscisse $\mathrm e^{-n-1}$.

b. Prouver que le point $A_{n}$ appartient à la droite $\Delta$ d'équation $y = x$.
Corrigé

L'ordonnée de $A_n$ est : \[\begin{aligned} f(\mathrm e^{-n-1}) &= -n\mathrm e^{-n-1} - \mathrm e^{n-1}\ln(\mathrm e^{-n-1})& \\ &= -n\mathrm e^{n-1} -(-n-1)\mathrm e^{-n-1}& \\ &= \mathrm e^{-n-1}.& \end{aligned}\] $A_n$ ayant une abscisse et une ordonnée identiques, il est bien sur la droite d'équation $y = x$.

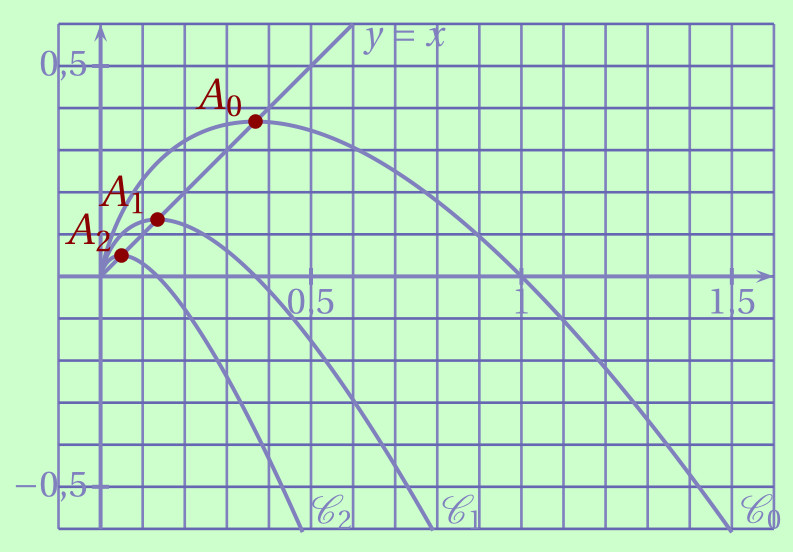
c. Placer sur la figure ci-dessous les points $A_{0}$, $A_{1}$ et $A_{2}$.
Corrigé

3.a. Démontrer que la courbe $\left(\mathcal{C}_{n}\right)$ coupe l'axe des abscisses en un unique point, noté $B_{n}$, dont l'abscisse est $\mathrm{e}^{-n}$.
Corrigé

$(\mathcal C_n)$ coupe l'axe des abscisses en un point d'abscisse $x$ si et seulement si : \begin{align*} f_n(x) &= 0&\\ \iff -nx - x\ln x &= 0&\\ \iff x\left(-n -\ln x\right) &= 0& \end{align*} Or $x\neq 0$ (car $f_n$ est définie sur $]0;+\infty[$), donc l'équation précédente équivaut à : \begin{align*} -n -\ln x &= 0&\\ \iff \ln x &= -n&\\ \iff x &=\mathrm e^{-n}.& \end{align*} La courbe $(C_n)$ coupe donc bien l'axe des abscisses en un unique point $B_n$ d'abscisse $\mathrm e^{-n}$.

b. Démontrer que la tangente à $\left(\mathcal{C}_{n}\right)$ au point $B_{n}$ a un coefficient directeur indépendant de l'entier $n$.
Corrigé

Le coefficient directeur de la tangente en $B_n$ à $\mathcal C_n$ est: \[\begin{aligned} f'(\mathrm e^{-n}) &= -n - 1 - \ln(\mathrm e^{-n})& \\ &=-n - 1 -(-n)& \\ &=-1.& \end{aligned}\] Cette tangente a donc un coefficient directeur égal à $-1$, indépendamment de la valeur de $n$.

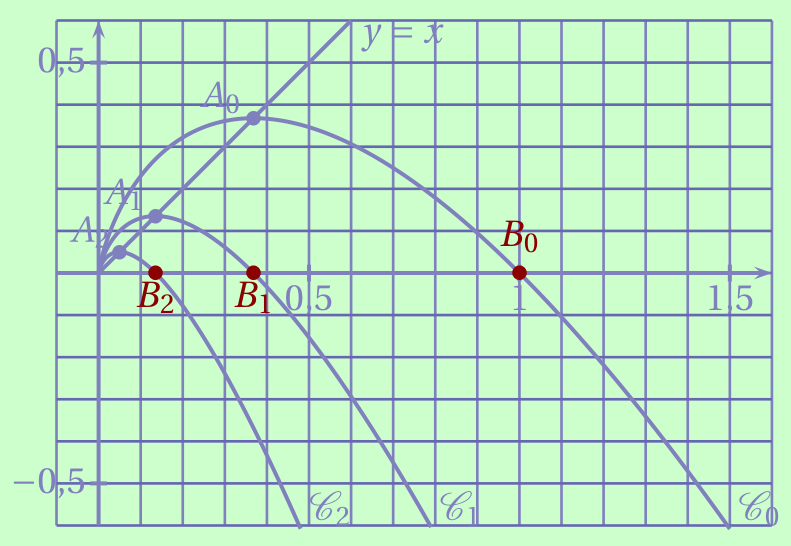
c. Placer sur la figure ci-dessous les points $B_{0}$, $B_{1}$ et $B_{2}$.
Corrigé

retour

code : 581