retour

1. Comparer les nombres : $a= 2^{2015}$ et $b=3^{1271}$.
   Corrigé
   Ces nombres dépassent la capacité de calcul de la plupart des machines.

   

   Calculons donc leurs logarithmes népériens : \[\begin{aligned} \ln(a) &=\ln\left(2^{2015}\right) = 2015\ln(2) \approx 1396,69& \\ \ln(b) &=\ln\left(3^{1271}\right) = 1271\ln(3) \approx 1396,34.& \end{aligned}\] La fonction ln étant strictement croissante : \[\ln(a) > \ln(b) \implies a > b.\]

   
2. Donner une valeur approchée du nombre $A = \dfrac{2^{2015}}{5^{867}}$.
   Corrigé
   Ici encore, utilisons le logarithme népérien : \[\begin{aligned} \ln\left(\frac{2^{2015}}{5^{867}}\right) &=\ln\left(2^{2015}\right) - \ln\left(5^{867}\right)& \\ &=2015\ln(2) - 867\ln(5)& \\ &\approx 1,3089.& \end{aligned}\] Donc \[A \approx \mathrm e^{1,3089} \approx 3,702.\]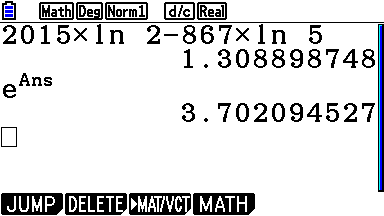

   

retour

code : 576