EX-20

retour

On considère la fonction \[f:x\mapsto \mathrm e^x - \dfrac 1 x\] définie et dérivable sur $\mathbb R^*$.

1. Déterminer une expression de la dérivée de $f$.
   Corrigé

   Pour tout $x\in\mathbb R^*$: \[f'(x) = \mathrm e^x -\left(-\frac 1 {x^2}\right) = \mathrm e^x + \frac 1 {x^2}.\]

2. Donner le signe de cette dérivée.
   Corrigé

   Pour tout $x\in\mathbb R^*$, $\mathrm e^x > 0$ et \[x^2 > 0 \implies \frac 1 {x^2} > 0\] Donc $f'(x) > 0$.

3. En déduire le tableau de variations de $f$ sur $\mathbb R^*$.
   Corrigé

   Limites aux bornes de l'ensemble de définition :
   En −∞ :
   $\displaystyle\lim_{x\to-\infty} \mathrm e^x = 0$ et $\displaystyle\lim_{x\to-\infty} \frac 1 x = 0$ donc $\displaystyle\lim_{x\to-\infty} f(x) = 0 + 0 = 0$.
   En 0^- :
   $\displaystyle\lim_{x\to 0^-} \mathrm e^x = 1$ et $\displaystyle\lim_{x\to 0^-} \frac 1 x = -\infty$ donc $\displaystyle\lim_{x\to 0^-} f(x) = 1 -(-\infty) = +\infty$.
   En 0⁺ :
   $\displaystyle\lim_{x\to 0^+} \mathrm e^x = 1$ et $\displaystyle\lim_{x\to 0^+} \frac 1 x = +\infty$ donc $\displaystyle\lim_{x\to 0^+} f(x) = 1 - (+\infty) = -\infty$.
   En +∞ : $\displaystyle\lim_{x\to+\infty} \mathrm e^x = +\infty$ et $\displaystyle\lim_{x\to+\infty} \frac 1 x = 0$ donc $\displaystyle\lim_{x\to+\infty} f(x) = (+\infty) + 0 = +\infty$.
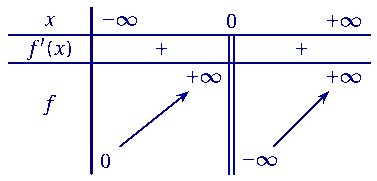
   On peut donc établir le tableau de variation suivant :
   

retour

code : 573