retour

Soit $k$ un nombre réel.

On considère la suite $\left(u_n\right)$ définie par son premier terme $u_0$ et pour tout entier naturel $n$, \[u_{n+1} = ku_n\left(1- u_n\right).\]

Les deux parties de cet exercice sont indépendantes. On y étudie deux cas de figure selon les valeurs de $k$.

Partie 1

Dans cette partie, $k = 1,9$ et $u_0 = 0,1$.
On a donc, pour tout entier naturel $n$, \[u_{n+1} = 1,9u_n\left(1 - u_n\right).\]

1. On considère la fonction $f$ définie sur $[0;1]$ par \[f(x) = 1,9x(1 - x).\]
   1. Étudier les variations de $f$ sur l'intervalle $[0;1]$.
      Corrigé
      Développons \[f(x) = 1,9x(1-x) = 1,9x - 1,9x^2.\] $f$ est dérivable sur $[0;1]$ et \[f'(x) = 1,9 - 1,9\cdot 2x = 1,9 - 3,8x.\] Étudions le signe de $f'(x)$: \[1,9 -3,8 x \ge 0 \iff \frac{1,9}{3,8} \ge x \iff \frac 1 2 \ge x.\] Donc :

      • Sur $\left[0;\frac 1 2\right]$, $f'$ est positive et donc $f$ est croissante ;
      • sur $\left[\frac 1 2;1\right]$, $f'$ est négative donc $f$ est décroissante.
   2. En déduire que si $x\in[0;1]$ alors $f(x)\in[0;1]$.
      Corrigé
      D'après les variations de $f$, son minimum est $f(0)$ ou $f(1)$. Or \[f(0)= f(1) = 0.\] Donc sur $[0;1]$, le minimum de la fonction $f$ est $0$.
      Toujours selon les variations de $f$, son maximum est \[f\left(\frac 1 2\right) = 1,9 \times \frac 1 2 \times \left(1-\frac 1 2\right) = 0,475.\] Puisque $0,475 < 1$, on peut affirmer que $f(x) \in [0;1]$.
2. Conjecturer le sens de variation de la suite $\left(u_n\right)$ et sa limite éventuelle.
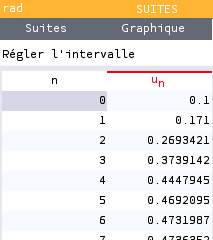
   Corrigé
   Calculons quelques termes de la suite $(u_n)$:
   $u_0 = 0,1$, $u_1 = 0,171$, $u_2 \approx 0,269$ … La suite $(u_n)$ semble croissante.

   Ses termes semble se rapprocher d'un nombre réel voisin de $0,47$. Elle semble donc convergente.
   

3. 1. En utilisant les résultats de la question 1, démontrer par récurrence que pour tout entier naturel $n$ : \[0 \leqslant u_n \le u_{n+1} \le \dfrac12.\] Corrigé
      Considérons l'assertion $\mathscr P(n)$ : «$0\le u_n \le u_{n+1} \le \frac 1 2$».
      Initialisation.$u_0 = 0,1$ et $u_1 = 0,171$, donc $0 \le u_0 \le u_1 \le \frac 1 2$. $\mathscr P(0)$ est donc vraie.
      Hérédité. Supposons $\mathscr P(n)$ vraie. Alors \[0 \le u_n \le u_{n+1} \le \frac 1 2.\] Puisque $f$ est croissante sur l'intervalle $\left[0;\frac 1 2\right]$, cela implique que : \[f(0) \le f(u_n) \le f(u_{n+1}) \le f\left(\frac 1 2\right).\] Or $f(0) = 0$ et $f\left(\frac 1 2\right) < \frac 1 2$, donc on a bien : \[0 \le u_{n+1} \le u_{n+2} \le \frac 1 2.\] On a bien $\mathscr P(n) \implies \mathscr P(n+1)$.
      Conclusion. Par récurrence, pour tout $n\in\mathbb N$, $0\le u_n \le u_{n+1} \le \frac 1 2$.

   2. En déduire que la suite $\left(u_n\right)$ converge vers un réel $\ell$.
      Corrigé
      La propriété précédente implique que la suite $(u_n)$ est croissante tout en étant majorée par $\frac 1 2$. Elle est donc convergente.
   3. Sachant que $f(\ell) = \ell$, déterminer $\ell$.
      Corrigé
      $\ell$ est solution de l'équation \[\begin{aligned} & f(x) = x &\\ \iff & 1,9x(1-x) = x &\\ \iff & 1,9x - 1,9x^2 - x = 0 &\\ \iff & -1,9x^2 + 0,9x = 0 &\\ \iff & x (-1,9x + 0,9) = 0.& \end{aligned}\] C'est un produit nul, donc :

      • Soit $x = 0$. Mais $u_0 = 0,1$ et la suite $(u_n)$ est croissante, donc elle ne peut pas converger vers $0$.
      • Soit $-1,9x + 0,9 = 0$ et donc \[x = \frac{-0,9}{-1,9} = \frac 9 {19}.\]

      Donc $\ell = \frac 9 {19}$.

Partie 2

Dans cette partie, $k= \dfrac12$ et $u_0 = \dfrac14$.
On a donc, pour tout entier naturel $n$, \[u_{n+1} = \dfrac12 u_n \left(1 - u_n\right).\] On admet que pour tout entier naturel $n$, \[0 \le u_n \le \left(\dfrac12\right)^n.\]

1. Démontrer que la suite $\left(u_n\right)$ converge et déterminer sa limite.
   Corrigé
   Puisque $\frac 1 2 \in \left]-1;1\right[$, on sait que \[\lim_{n\to+\infty} \left(\frac 1 2\right)^n = 0.\] La suite $(u_n)$ est donc encadrée par deux suites tendant vers 0. Elle converge donc elle aussi vers 0 (th. des gendarmes).
2. On considère la fonction Python algo(p) où p désigne un entier naturel non nul :
   def algo(p) : u =1/4 n = 0 while u > 10**(-p): u = 1/2*u*(1 - u) n = n+1 return(n)
   Expliquer pourquoi, pour tout entier naturel non nul p, la boucle while ne tourne pas indéfiniment, ce qui permet à la commande algo(p) de renvoyer une valeur.
   Corrigé
   La fonction python algo(p) renvoie le rang $n$ du premier terme tel que $u_n \le 10^{-p}$.
   Puisque la suite $(u_n)$ tend vers $0$, quel que soit $p$, il y aura bien un terme de la suite $(u_n)$ vérifiant $u_n \le 10^{-p}$.
   La fonction devrait donc toujours renvoyer une valeur.

retour

code : 571