retour

Le nombre de pains produits à l'heure dans une boulangerie industrielle, en dizaines de milliers, en fonction du nombre $n$ de travailleurs employés, en centaine d'employés, vérifie la relation \[P(n) = \frac 3 8 n^2 - \frac 1 {32} n^3.\]

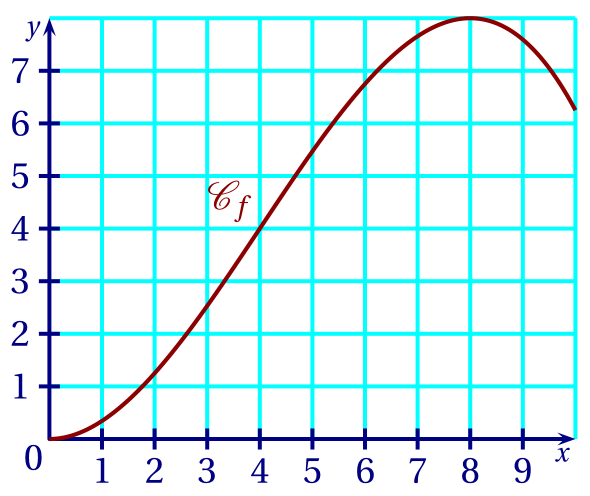
Voici, dans un repère, la courbe représentative $\mathscr C_f$ de la fonction $f$ définie sur $[0;10]$ par: \[f(x) = \dfrac 3 8 x^2 - \dfrac 1 {32} x^3.\]

1. Conjecturer graphiquement le nombre d'employés à partir duquel la croissance de production diminue.
   Corrigé
   On cherche le moment où la fonction passe de convexe (la croissance s'accélère) à concave (la croissance ralentit). Il semble que ce soit au point d'abscisse 4 (donc pour 400 employés).
   La détermination précise de cette abscisse est délicate, car la courbe est quasiment rectiligne autours de ce point.
2. Déterminer la fonction dérivée seconde de $f$ et démontrer la conjecture précédente.
   Corrigé
   La fonction $f$ est une fonction polynôme, donc dérivable sur $[0\;;\;10]$ autant de fois qu'on le voudra. \begin{flalign*} f'(x) &=\frac 3 8 \cdot 2x - \frac 1 {32}\cdot 3x^2 = \frac 3 4 x - \frac 3 {32} x^2\;;& \\ f''(x)&=\frac 3 4 - \frac 3 {32}\cdot 2x = \frac 3 4 - \frac 3 {16} x.& \end{flalign*} Étudions le signe de $f''(x)$. $f''$ est une fonction affine qui s'annule quand \begin{align*} f''(x) &= 0& \\ \iff \frac 3 4 - \frac 3 {16} x &= 0& \\ \iff x &= -\frac 3 4 \times \left(-\frac {16} 3\right)& \\ \iff x &= 4.& \end{align*} Son coefficient directeur est $-\frac 3{16}$. Il est négatif, donc $f''$ est positive sur $[0;4]$ puis négative sur $[4;10]$.
   $f$ est donc convexe sur $[0;4]$ puis concave sur $[4;10]$. Elle admet bien un point d'inflexion d'abscisse 4.
   C'est donc bien à partir de 400 employés que les gains de productivité commencent à diminuer.

retour

code : 564