retour

$f$ est la fonction définie sur $[0;+\infty[$ par \[f(x) = \sqrt x\] et $\mathscr C$ est sa courbe représentative dans un repère.

1. Déterminer une équation de la tangente $T$ à $\mathscr C$ au point d'abscisse 4.
   Corrigé
   D'une part, \[f(4) = \sqrt{4} = 2.\] D'autre part, la fonction $f$ est dérivable sur $]0;+\infty[$ et pour tout réel de cet intervalle: \[f'(x) = \frac 1 {2\sqrt x}.\] On en déduit donc que \[f'(4) = \frac{1}{2\sqrt 4} = \frac 1 {2\times 2} = \frac 1 4.\] L'équation de $T$ est donc \[\begin{aligned} y &= f'(4)(x-4) + f(4)& \\ \iff y &= \frac 1 4(x-4) + 2& \\ \iff y &= \frac 1 4 x - 1 + 2& \\ \iff y &= \frac 1 4 x + 1.& \end{aligned}\]
2. Sur une calculatrice graphique, tracer $\mathscr C$ et $T$.
   Corrigé
   Copie d'écran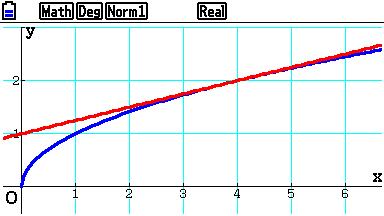

retour

code : 563