EX-36
retour
En 2020, la population d'un animal en voie d'extinction est estimée à 100 000 individus.
En supposant que, chaque année, cette population diminue de 10%,
au bout de combien d'années sera-t-elle réduite à moins de 1000 individus ?
Début corrigé
fin (méthode heuristique)
fin (résolution d'inéquation)
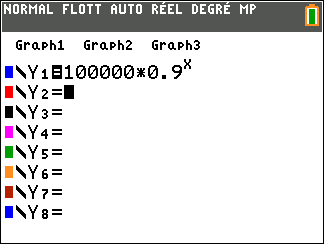
Chaque année, cette population est multipliée par $1-\dfrac{10}{100} = 0,9$.
Donc la population au bout de $n$ années est donnée par \[p(n) = 100000 \times 0,9^n.\] On cherche donc $n$ tel que : $p(n) < 1000$.
Donc la population au bout de $n$ années est donnée par \[p(n) = 100000 \times 0,9^n.\] On cherche donc $n$ tel que : $p(n) < 1000$.
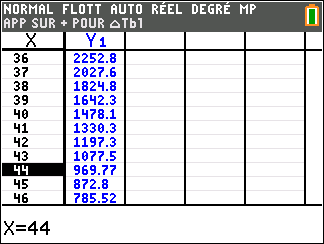
On effectue une recherche à l'aide de la calculatrice.
On obtient que $p(43)\approx 1078$ tandis que $p(44) \approx 970$.
C'est donc au bout de 44 ans que la population sera réduite à moins de 1000 individus.
On obtient que $p(43)\approx 1078$ tandis que $p(44) \approx 970$.
C'est donc au bout de 44 ans que la population sera réduite à moins de 1000 individus.


\begin{align*}
100000 \times 0,9^n &< 1000&
\\ \iff
0,9^n &<\frac{1000}{100000}&
\\ \iff
0,9^n &< 0,01&
\\ \iff
\ln(0,9^n) &<\ln(0,01)&
\\ \iff
n\ln(0,9) &< \ln(0,01)&
\\ \iff
n &> \frac{\ln(0,01)}{\ln(0,9)}.&
\end{align*}
Or $\dfrac{\ln(0,01)}{\ln(0,9)} \approx 43,7$, donc c'est au bout de 44 ans que la population
sera réduite à moins de 1000 individus.

retour
code : 56