retour

Une jardinerie vend de jeunes plants d'arbres qui proviennent de trois horticulteurs :

35 % des plants proviennent de l'horticulteur H₁, 25 % de l'horticulteur H₂ et le reste de l'horticulteur H₃.

Chaque horticulteur livre deux catégories d'arbres : des conifères et des arbres à feuilles.

La livraison de l'horticulteur H₁ comporte 80 % de conifères alors que celle de l'horticulteur H₂ n'en comporte que 50 % et celle de l'horticulteur H₃ seulement 30 %.

1. Le gérant de la jardinerie choisit un arbre au hasard dans son stock. On envisage les événements suivants :
   • $H_{1}$ : « l'arbre choisi a été acheté chez l'horticulteur $\mathrm H_{1}$ »,
   • $H_{2}$ : « l'arbre choisi a été acheté chez l'horticulteur $\mathrm H_{2}$ »,
   • $H_{3}$ : « l'arbre choisi a été acheté chez l'horticulteur $\mathrm H_{3}$ »,
   • $C$: « l'arbre choisi est un conifère »,
   • $F$: « l'arbre choisi est un arbre feuillu ».
   1. Construire un arbre pondéré traduisant la situation.
      Corrigé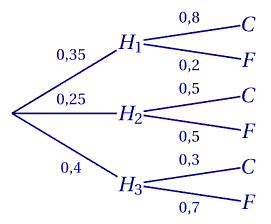
      
   2. Calculer la probabilité que l'arbre choisi soit un conifère acheté chez l'horticulteur H₃.
      Corrigé
      \[\begin{aligned} P(H_3\cap C) &= P(H_3)\times P_{H_3}(C)&\\ &= 0,4\times 0,3&\\ &= 0,12.& \end{aligned}\]
   3. Justifier que la probabilité de l'évènement $C$ est égale à 0,525.
      Corrigé
      Selon la loi des probabilités totales: \[\begin{aligned} P(C) &= P(H_1\cap C) + P(H_2\cap C) + P(H_3 \cap C)&\\ &=0,35 \times 0,8 + 0,25\times 0,5 + 0,12&\\ &=0,525.& \end{aligned}\]
   4. L'arbre choisi est un conifère. Quelle est la probabilité qu'il ait été acheté chez l'horticulteur H₁ ? On arrondira à 10⁻³.
      Corrigé
      On cherche: \[P_C(H_1) = \dfrac{P(C\cap H_1)}{P(C)}=\dfrac{0,35 \times 0,8}{0,525} \approx 0,533.\]
2. On choisit au hasard un échantillon de 10 arbres dans le stock de cette jardinerie. On suppose que ce stock est suffisamment important pour que ce choix puisse être assimilé à un tirage avec remise de 10 arbres dans le stock.
   On appelle $X$ la variable aléatoire qui donne le nombre de conifères de l'échantillon choisi.
   1. Justifier que $X$ suit une loi binomiale dont on précisera les paramètres.
      Corrigé
      Le tirage est supposé avec remise, donc chaque choix d'arbre est indépendant des autres et a la même probabilité d'aboutir au choix d'un conifère.
      $X$ suit donc bien la loi binomiale de paramètres $n=10$ et $p=0,525$.
   2. Quelle est la probabilité que l'échantillon prélevé comporte exactement 5 conifères ?
      On arrondira à 10⁻³.
      Corrigé
      \[ P(X = 5) \approx 0,243.\] (d'après la calculatrice.)
   3. Quelle est la probabilité que cet échantillon comporte au moins deux arbres feuillus ?
      On arrondira à 10⁻³.
      Corrigé
      Au moins deux feuillus signifie au plus 8 conifères. On cherche donc : \[P(X\le 8) \approx 0,984.\] (d'après la calculatrice.)

retour

code : 557