EX-

retour

Les trois parties A, B et C peuvent être traitées de façon indépendante.

Un élève doit se rendre à son lycée chaque matin pour 8 h 00. Pour cela, il utilise, selon les jours, deux moyens de transport : le vélo ou le bus.

Partie A

L'élève part tous les jours à 7 h 40 de son domicile et doit arriver à 8 h 00 à son lycée.

Il prend le vélo 7 jours sur 10 et le bus le reste du temps.

Les jours où il prend le vélo, il arrive à l'heure dans 99,4% des cas et lorsqu'il prend le bus, il arrive en retard dans 5% des cas.

On choisit une date au hasard en période scolaire et on note

$V$ l'évènement « L'élève se rend au lycée à vélo »;
$B$ l'évènement « l'élève se rend au lycée en bus »;
$R$ l'évènement « L'élève arrive en retard au lycée ».

1. Traduire la situation par un arbre de probabilités.
Corrigé

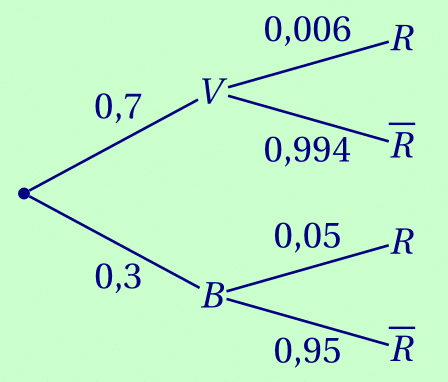
2. Déterminer la probabilité de l'évènement $V \cap R$.
Corrigé

\[P(V\cap R) = P(V)\times P_V(R) = 0,7\times 0,006 = 0,0042.\]

3. Démontrer que la probabilité de l'évènement $R$ est 0,0192.
Corrigé

Selon la formule des probabilités totales \begin{align*} P(R) &=P(V\cap R) +P(B\cap R)& \\ &=0,0042 + P(B)\times P_B(R)& \\ &=0,0042 + 0,3 \times 0,05& \\ &=0,0042 + 0,015& \\ &=0,0192.& \end{align*}

4. Un jour donné, l'élève est arrivé en retard au lycée. Quelle est la probabilité qu'il s'y soit rendu en bus ?
Corrigé

\[P_R(B) = \dfrac{P(B\cap R)}{P(R)} = \dfrac{0,015}{0,0192} = 0,78125.\]

Partie B : le bus

On suppose dans cette partie que l'élève utilise le bus pour se rendre à son lycée.

Lorsqu'il utilise le bus, on modélise son temps de parcours, exprimé en minutes, entre son domicile et son lycée par la variable aléatoire $T$ doit la loi est donnée ci-dessous. \[\small \begin{array}{|l|*{8}{c|}}\hline t & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 \\ \hline P(T=t)& 0,04 & 0,11 & 0,19 & 0,31 & 0,22 & 0,08 & 0,03& 0,02 \\ \hline \end{array}\]

1. Déterminer $P(T \le 18)$.
Corrigé

\[P(T\le 18) = 0,04 + 0,11 + 0,19 + 0,31 = 0,65.\]

2. Calculer, arrondie à la minute près, la durée moyenne d'un trajet en bus.
Corrigé

\[\operatorname E(T) = 0,04\times 15 + 0,11\times 16 + \cdots + 0,02\times 22 \approx 18.\] Son trajet dure en moyenne 18 minutes.

Partie C : le vélo

On suppose dans cette partie que l'élève utilise le vélo pour se rendre à son lycée.

Dans cette partie, les probabilités pourront être arrondies au millième.

Lorsqu'il utilise le vélo, on modélise son temps de parcours, exprimé en minutes, entre son domicile et son lycée par \[T' = 15 + X\] où $X$ est une variable aléatoire qui suit le loi binomiale de paramètres $n = 10$ et $p=0,198$.

1. Déterminer la probabilité que l'élève arrive à 7 h 58 au lycée.
Corrigé

\[P(T'=18) = P(X=3) \approx 0,199.\] (Obtenu à la calculatrice.)

2. Déterminer la probabilité que l'élève mette entre 15 et 20 minutes pour se rendre à son lycée.
Corrigé

\[P(15 \leqslant T'\leqslant 20) = P(X\leqslant 5) \approx 0,994.\] (Obtenu à la calculatrice.)

3. Quel est, en moyenne, le temps de parcours de cet élève ?
Corrigé

\[\operatorname E(X) = np = 10\times 0,198 \approx 2.\] Donc le temps moyen est d'environ 15+2 = 17 minutes.

4. Il part de son domicile à vélo à 7 h 40. Quelle est la probabilité qu'il soit en retard au lycée ?
Corrigé

\[\begin{aligned} P(T'>20) &= P(X > 5)& \\ &= 1 - P(X\leqslant 5)& \\ &\approx 1 - 0,994& \\ &\approx 0,006.& \end{aligned}\]

retour

code : 555