EX-

retour

Une entreprise fabrique des billes en bois sphériques grâce à deux machines de production A et B.
L'entreprise considère qu'une bille peut être vendue uniquement lorsque son diamètre est compris entre 0,9 cm et 1,1 cm.

Les parties A et B sont indépendantes.

Partie A

Une étude du fonctionnement des machines a permis d'établir les résultats suivants :

96% de la production journalière est vendable.
La machine A fournit 60% de la production journalière.
La proportion de billes vendables parmi la production de la machine A est 98%.

On choisit une bille au hasard dans la production d'un jour donné. On définit les évènements suivants :

$A$ : «la bille a été fabriquée par la machine A»;
$B$ : «la bille a été fabriquée par la machine B»
$V$ : «la bille est vendable».

1. L'arbre de probabilités ci-dessous modélise la situation. Quelles sont les valeurs des réels $p_1$, $p_2$, $p_3$ et $p_4$?
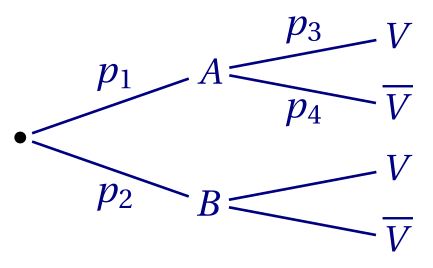
arbre
Corrigé

D'après la consigne, \[p(A)=p_1 = 0,6\] et \[P_A(V) = p_3 = 0,98.\]
On en déduit que $p_2 = 1-0,6 = 0,4$ et $p_4 = 1-0,98 = 0,02$.

2. Déterminer la probabilité que la bille choisie soit vendable et provienne de la machine A.
Corrigé

$P(A\cap V) = P(A)\times P_A(V) = 0,6 \times 0,98 = 0,588$.

3.a. Justifier que $P(B \cap V) = 0,372$.
Corrigé

\[\begin{aligned} &P(V) = P(A\cap V) + P(B\cap V)&\\ \iff &0,96 = 0,588 + P(B\cap V)&\\ \iff &P(B\cap V) = 0,96 - 0,588 = 0,372.& \end{aligned}\]

3.b. En déduire la probabilité que la bille choisie soit vendable sachant qu'elle provient de la machine B.
Corrigé

$P_B(V)=\dfrac{P(B\cap V)}{P(B)}=\dfrac{0,372}{0,4} = 0,93$.

4. Un technicien affirme que 70% des billes non vendables proviennent de la machine B. A-t-il raison?
Corrigé

Remarquons d'abord que : \[P_B\left(\overline V\right) = 1-P_B(V) = 1 - 0,93 = 0,07.\] Donc : \[\begin{aligned} P_{\overline V}(B) &= \frac{P\left(B\cap\overline V\right)}{P\left(\overline V\right)} =\frac{P(B)\times P_B\left(\overline V\right)}{1-P(V)}& \\ &=\frac{0,4\times 0,07}{1-0,96} =\frac{0,028}{0,04} =0,7.& \end{aligned}\] Donc le technicien a raison.

Partie B

Les billes vendables passent ensuite dans une machine qui les teinte de manière aléatoire et équiprobable en blanc, noir, bleu, jaune ou rouge.
Après avoir été mélangées, les billes sont conditionnées en sachets.
La quantité produite est suffisamment importante pour que le remplissage d'un sachet puisse être assimilé à un tirage successif avec remise de billes dans la production journalière.
Une étude de consommation montre que les enfants sont particulièrement attirés par les billes de couleur noire.

1. Dans cette question seulement, les sachets sont tous composés de 40 billes.

a. On note $X$ la variable aléatoire donnant le nombre de billes de couleur noire dans un sachet. Quelle est la loi de probabilité suivie par $X$? Justifier.
Corrigé

Tirage assimilé à un tirage avec remise donc $X$ suit loi binomiale de paramètres $n = 40$ et $p=\frac 1 5 = 0,2$.

b. On choisit au hasard un sachet de billes. Déterminer la probabilité que le sachet choisi contienne exactement 10 billes noires. On arrondira le résultat à 10⁻³.
Corrigé

D'après la calculatrice, $P(X=10) \approx 0,107$.

2. Si l'entreprise souhaite que la probabilité d'obtenir au moins une bille noire dans un sachet soit supérieure ou égale à 99%, quel nombre minimal de billes chaque sachet doit-il contenir pour atteindre cet objectif?
Corrigé 1 Corrigé 2

On fait des essais à la calculatrice en lui demandant de calculer $P(X = 0)$ avec différentes valeurs de $n$.
On constate que \[\begin{aligned} &n = 20 \implies P(X = 0) \approx 0,012 \implies P(X=0) > 0,01&\\ &n=21 \implies P(X=0) \approx 0,007 \implies P(X=0) < 0,01.& \end{aligned}\] Donc $n = 21$.

On sait que \[P(X=0) = (1-p)^n = (1 - 0,2)^n = 0,8^n.\] On cherche donc à avoir \[\begin{aligned} 0,8^n &\leqslant 0,01& \\ \iff \ln\left(0,8\right)^n &\leqslant \ln 0,01& \\ \iff n\ln 0,8 &\leqslant \ln 0,01& \\ \iff n &\geqslant \frac{\ln 0,01}{\ln 0,8}.& \end{aligned}\] Or $\dfrac{\ln 0,01}{\ln 0,8} \approx 20,64$, donc $n = 21$.

retour

code : 554