retour

Donner la valeur exacte des cinq premiers termes de chacune des suites proposées.

1. La suite $(a_n)$, de premier terme $a_1$, est définie comme la suite des décimales de $\sqrt 3$.
   Corrigé
   D'après la calculatrice, \[\sqrt{3} \approx 1,7320508\ldots\] donc \[\begin{aligned} a_1 &= 1\;;& \ a_2 &= 3\;;& \ a_3 &= 2\;;& \\ a_4 &= 0\;;& \ a_5 &= 5.& \end{aligned}\]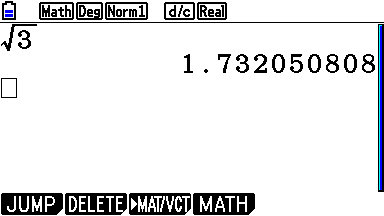

   
2. La suite $(b_n)$ est définie pour tout entier naturel $n$ par \[b_n = (-2)^n.\] Corrigé
   \[\begin{aligned} b_0&=(-2)^0 = 1\;;& b_1&=(-2)^1 = -2\;;& \\ b_2&=(-2)^2 = 4\;;& b_3&=(-2)^3 = -8\;;& \\ b_4&=(-2)^4=16.& \end{aligned}\]
3. La suite $(c_n)$ est telle que pour tout entier naturel non nul, $c_n$ est l'inverse du nombre $n$.
   Corrigé
   \[\begin{aligned} c_1&= \frac 1 1 = 1\;;& c_2 &= \frac 1 2\;;& c_3 &= \frac 1 3\;;& \\ c_4 &= \frac 1 4\;;& c_5 &= \frac 1 5.& \end{aligned}\]

retour

code : 445