7.05

retour

On considère l'équation d'inconnue $x$ réelle: \[\mathrm{e}^{x}=3\left(x^2+x^3\right).\tag{E}\]

Partie A: Conjecture graphique

Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction $f$ définie sur $\mathbb{R}$ par \[f(x)=3(x^2+x^3)\] telles que les affiche une calculatrice dans un même repère orthogonal.

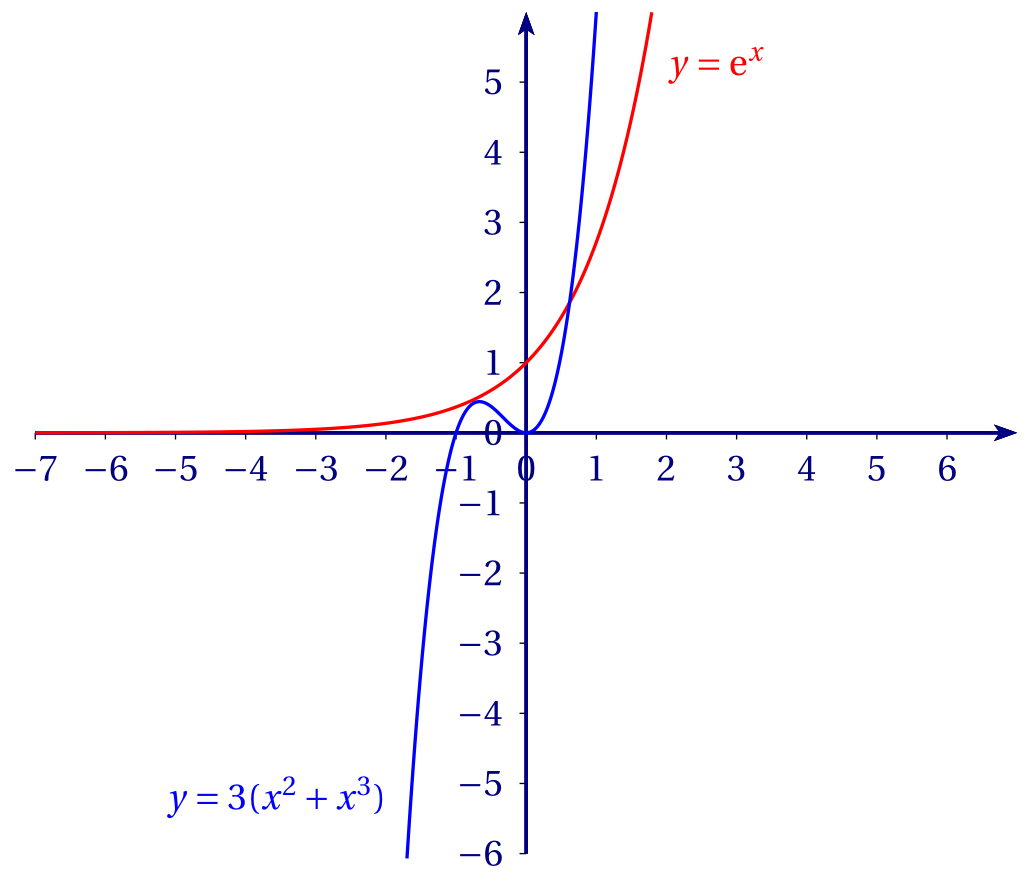
À l'aide du graphique ci-dessus, conjecturer le nombre de solutions de l'équation (E) et leur encadrement par deux entiers consécutifs.
Corrigé

Les courbes des deux fonctions semblent se couper en deux points, donc on pourrait supposer qu'il y a deux solutions $x_1$ et $x_2$ à l'équation (E), telles que \[-1< x_1 < 0\quad\text{et}\quad 0 < x_2 < 1.\]

Partie B: étude de la validité de la conjecture graphique

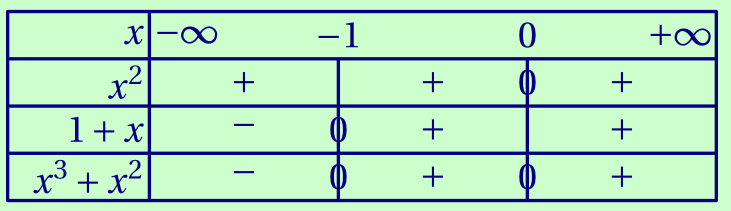
1.a Étudier selon les valeurs de $x$, le signe de $x^2+x^3$.
Corrigé

On a: $x^2+x^3 = x^2(1+x)$, donc on peut réaliser l'étude de signe :
tableau de signes

1.b. En déduire que l'équation (E) n'a pas de solution sur l'intervalle $]-\infty;-1]$.
Corrigé

Puisque pour tout réel $x$, $\mathrm e^x>0$, on ne peut avoir \[x^3+x^2 = \mathrm e^x\] quand $x^3+x^2$ est strictement négatif, donc d'après l'étude de signe précédente, l'équation est sans solution sur $]-\infty;-1]$.

1.c. Vérifier que 0 n'est pas solution de (E).
Corrigé

On vient de préciser que pour tout réel $x$, $\mathrm e^x \neq 0$.
Donc puisque $x^3+x^2$ est nulle en $0$, $0$ ne peut être solution de (E).

2. On considère la fonction $h$, définie pour tout nombre réel de $]-1;0[\cup]0;+\infty[$ par: \[h(x)=\ln 3+\ln\left(x^2\right)+\ln(1+x)-x.\] Montrer que, sur $]-1;0[\cup]0;+\infty[$, l'équation (E) équivaut à $h(x) = 0$.
Corrigé

\begin{flalign*} &\mathrm e^x = 3\left(x^2 + x^3\right)& \\ \iff &x = \ln\left[3\left(x^2 + x^3\right)\right]& \\ \iff &x = \ln 3 + \ln\left(x^2(1+x)\right)& \\ \iff &x = \ln 3 + \ln x^2 + \ln(1+x)& \\ \iff &x = \ln 3 +\ln x^2 + \ln(1+x)& \\ \iff &\ln 3 +\ln x^2 + \ln(1+x) - x = 0& \\ \iff &h(x) = 0.& \end{flalign*}

3.a Montrer que, pour tout réel $x$ appartenant à $]-1;0[\cup]0;+\infty[$, on a: \[h'(x)=\dfrac{-x^2+2x+2}{x(x+1)}.\]
Corrigé

$h$ est dérivable sur $]-1;0[\cup]0;+\infty[$ comme somme de fonctions dérivables sur cet intervalle : \begin{flalign*} h'(x) &= 0 + \frac{2x}{x^2} + \frac{1}{1+x} - 1 = \frac 2 x +\frac 1 {1+x} - 1& \\ &=\frac{2(1+x) + x - x(1+x)}{x(1+x)}& \\ &=\frac{2+2x + x -x^2 - x}{x(1+x)}& \\ &=\frac{-x^2 +2x +2}{x(1+x)}.& \end{flalign*}

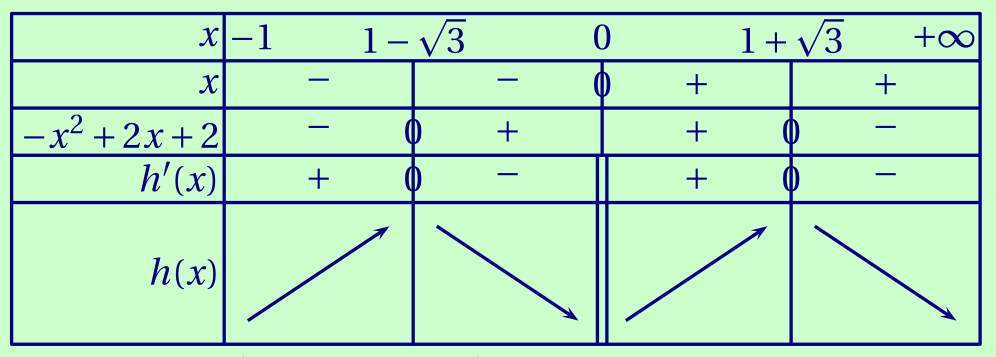
3.b. Déterminer les variations de la fonction $h$.
Corrigé

Considérons le polynôme de degré 2 $-x^2 + 2x + 2$.
Son discriminant, $\Delta = 2^2 - 4\times(-1)\times 2 = 12$ est strictement positif, donc il admet deux racines: \begin{flalign*} x_1 &= \frac{-2+\sqrt{12}}{-2} = \frac{-2+2\sqrt 3}{-2} = 1-\sqrt 3;amp; \\ x_2 &= \frac{-2-\sqrt{12}}{-2} = \frac{-2-2\sqrt 3}{-2} = 1+\sqrt 3.amp; \end{flalign*} Son coefficient principal est négatif, donc il est négatif à l'extérieur de ses racines.
D'autre part, $(x+1)$ est strictement positive sur $]-1;0[\cup]0;+\infty[$, donc ce facteur ne modifie pas le signe de $h'(x)$. On a alors le tableau :
tableau

3.c. On admet que $\displaystyle\lim_{x\to +\infty} h(x) = -\infty$. Montrer que $\displaystyle\lim_{x\to 0} h(x) = -\infty$
Corrigé

Puisque $\displaystyle\lim_{x\to 0} x^2 = 0^+$, $\displaystyle\lim_{x\to 0} \ln x^2 = -\infty$ et puisque $\displaystyle \lim_{x\to 0} x + 1 = 1$, $\displaystyle\lim_{x\to 0} \ln(x+1) = 0$.
On a donc : \[\lim_{x\to 0} h(x) = -\infty.\]

3.d. Déterminer le nombre de solutions de l'équation $h(x)=0$ et donner une valeur arrondie au centième de chaque solution.
Corrigé

D'après le tableau de variation, $h$ admet un maximum sur $]-1;0[$ en $1-\sqrt 3$. Or $f(1-\sqrt 3) \approx -0,11$, donc $h$ est strictement négative sur cet intervalle.
On a $h(1+\sqrt 3) \approx 1,7$. Donc :

sur $]0;1+\sqrt 3$, $h$ est strictement croissante, continue et $\displaystyle\lim_{x\to 0} h(x) = -\infty< 0$ tandis que $h(1+\sqrt 3) >0$.
$h(x) = 0$ admet donc une unique solution $\alpha_1$ sur cet intervalle;
sur $]1+\sqrt 3;+\infty[$, $h$ est strictement décroissante, continue et $f(1+\sqrt 3)>0$ tandis que $\displaystyle\lim_{x\to +\infty} h(x) = -\infty<0$.
$h(x) = 0$ admet donc aussi une unique solution $\alpha_2$ sur cet intervalle.

De $h(0,618)\approx -0,0007$ et $h(0,619)\approx 0,002$, on déduit que $\alpha_1 \approx 0,62$.
De $h(7,118)\approx 0,0006$ et $h(7,119)\approx -0,0005$, on déduit que $\alpha_2 \approx 7,12$.

3.e. Conclure quant à la conjecture de la partie A.
Corrigé

La solution conjecturée entre −1 et 0 se révèle fausse. Les courbes ne se coupent pas en ce point.
La solution conjecturée entre 0 et 1 est fondée : c'est $\alpha_1$.
Il existe enfin une autre solution, $\alpha_2$, qui n'apparaît pas dans la fenêtre graphique proposée.

retour

code : 412