retour

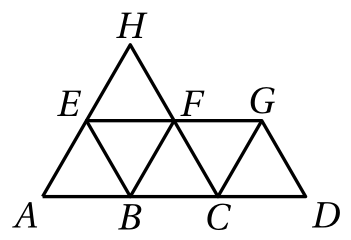
On considère la figure ci-dessous dans laquelle les triangles tracés sont équilatéraux.

1. Recopier et compléter les égalités suivantes avec des points de la figure.
   1. $\overrightarrow{AB}+\overrightarrow{BE} = \overrightarrow{A\cdots}$;
      Corrigé
      $\overrightarrow{AB}+\overrightarrow{BE} = \overrightarrow{\mathbf AE}$.
   2. $\overrightarrow{AB}-\overrightarrow{FB} = \overrightarrow{A\cdots}$;
      Corrigé
      $\overrightarrow{AB}-\overrightarrow{FB} = \overrightarrow{AB}+\overrightarrow{BF} = \overrightarrow{\mathbf AF}$.
   3. $\overrightarrow{HE}+\overrightarrow{DG} = \overrightarrow{F\cdots}$;
      Corrigé
      $\overrightarrow{HE}+\overrightarrow{DG} = \overrightarrow{FB}+\overrightarrow{BE} =\overrightarrow{\mathbf FE}$.
   4. $\overrightarrow{FC} - \overrightarrow{CB} = \overrightarrow{F\cdots}$.
      Corrigé
      $\overrightarrow{FC} - \overrightarrow{CB} = \overrightarrow{FC}+\overrightarrow{CD} = \overrightarrow{\mathbf FD}$.
2. Remplacer les sommes vectorielles suivantes par un vecteur unique.
   1. $\overrightarrow{CE}+\overrightarrow{AC}$;
      Corrigé
      $\overrightarrow{CE}+\overrightarrow{AC} = \overrightarrow{AC}+\overrightarrow{CE} = \overrightarrow{AE}$
   2. $\overrightarrow{EF}-\overrightarrow{FC}$;
      Corrigé
      $\overrightarrow{EF}-\overrightarrow{FC} =\overrightarrow{EF}+\overrightarrow{FH} =\overrightarrow{EH}$
      (ou encore $\overrightarrow{AE}$, $\overrightarrow{BF}$, $\overrightarrow{CG}$).
   3. $-\overrightarrow{BA} + \overrightarrow{AC}$;
      Corrigé
      $-\overrightarrow{BA} + \overrightarrow{AC} =\overrightarrow{AB}+\overrightarrow{BD} = \overrightarrow{AD}$.
   4. $\overrightarrow{AB}+\overrightarrow{AE}+\overrightarrow{BC}$.
      Corrigé
      $\overrightarrow{AB}+\overrightarrow{AE}+\overrightarrow{BC} =\overrightarrow{AB}+\overrightarrow{BF}+\overrightarrow{FG} = \overrightarrow{AG}$

retour

code : 403