387
retour
On ne demande pas de refaire la figure.
ABCDEFGH est un cube dont l'arête a pour longueur 3 cm.
K est un point de l'arête [DH].
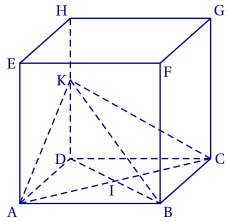
On considère la pyramide de sommet K et de base ABCD ; sa hauteur est le segment [KD].
Partie A
Dans cette partie, K est le milieu de l'arête [DH].
-
-
Quelle est la nature du triangle ABD ?
Justifier la réponse.
Corrigé[AB] et [AD] sont deux arêtes contigües du cube, elles sont donc perpendiculaires et de même longueur. Donc ABD est un triangle rectangle isocèle en A. -
Démontrer que $\mathrm{DB}=3\sqrt 2$. Déterminer l'arrondi de DB à
0,1 près.
CorrigéPuisque ABD est un triangle isocèle en A, le théorème de Pythagore permet d'affirmer que \[\begin{aligned} &\mathrm{DB}^2 = \mathrm{AB}^2 + \mathrm{AD}^2 = 3^2 + 3^2 = 9 + 9 = 18;& \\ \implies &\mathrm{BD} = \sqrt{18} = \sqrt{9\times 2} = \sqrt 3 \times \sqrt 2 = 3\sqrt 2\ \text{cm}& \end{aligned}\] D'après la calculatrice, DB≈4,2cm.
-
Quelle est la nature du triangle ABD ?
-
On considère le triangle HDB, rectangle en D.
-
Calculer la valeur exacte de HB.
CorrigéPuisque le triangle HDB est rectangle en D, on peut à nouveau appliquer le théorème de Pythagore \[\begin{aligned} \mathrm{HB}^2 &= \mathrm{HD}^2 + \mathrm{DB}^2 =3^2 + \left(\sqrt{18}\right)^2 =9 + 18 =27;& \\ \implies &HB = \sqrt{27} = \sqrt{9\times 3} = \sqrt 9 \times \sqrt 3 = 3\sqrt 3\ \text{cm}& \end{aligned}\] -
Le point I est le centre du carré ABCD.
Que représente I pour le segment [BD] ? Pourquoi ?
CorrigéLa face ABCD est un carré et les diagonales d'un carré se coupent en leur milieu donc I est le milieu de [BD]. -
Démontrer que les droites (KI) et (HB) sont parallèles.
CorrigéConsidérons le triangle DBH.I est le milieu de [DB] donc D, I et B sont alignés dans cet ordre avec \[\dfrac{\mathrm{DI}}{\mathrm{DB}}=\dfrac 1 2.\] K est le milieu de [DH] donc D, K et H sont alignés dans cet ordre avec \[\dfrac{\mathrm{DK}}{\mathrm{DH}}=\dfrac 1 2.\] Donc \[ \dfrac{\mathrm{DI}}{\mathrm{DB}}=\dfrac{\mathrm{DK}}{\mathrm{DH}}.\] Selon la réciproque du théorème de Thalès, les droites (IK) et (BH) sont donc bien parallèles.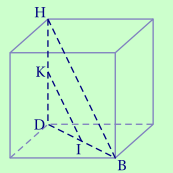
-
Calculer la valeur exacte de HB.
Partie B
Dans cette partie, le point K a une position quelconque sur l'arête [DH] ;
$x$ désigne la longueur, en cm, de DK et $f(x)$ le volume, en cm3,
de la partie du cube qui n'est pas occupée par la pyramide KABCD.
-
-
Quelles sont les valeurs possibles de $x$ ?
CorrigéPuisque K∈[DK], x∈[0;3]. -
Exprimer le volume de la pyramide KABCD en fonction de $x$.
CorrigéSi ABCD est la base, il s'agit d'un carré d'aire (en cm2) : \[\mathscr A_{\mathrm{ABCD}} = \mathrm{AB}^2 = 3^2 = 9.\] La hauteur associée à cette base est [DK] de longueur x.
Donc le volume de la pyramide (en cm3) est \[\frac 1 3 \times \mathscr A_{\mathrm{ABCD}} \times \mathrm{DK} =\frac 1 3 \times 9 \times x =3x.\] -
En déduire que $f(x) =27 - 3x$.
CorrigéLe volume (en cm3) du cube est \[\mathrm{AB}^3 = 3^3 = 27.\] Donc le volume non occupé par la pyramide vaut \[f(x) = 27 - 3x.\]
-
Quelles sont les valeurs possibles de $x$ ?
-
Le plan est rapporté à un repère orthogonal.
Représenter graphiquement le volume $f(x)$ en fonction de la longueur $x$.
CorrigéOn reconnaît en $f$ une fonction affine, qui sera donc représentée par un segment de droite.
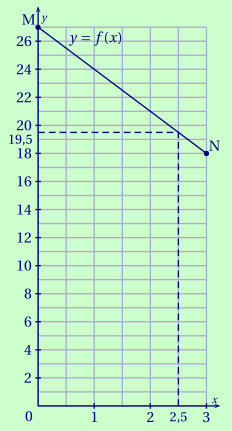
Choisissons les valeurs extrêmes pour $x$ \[\begin{aligned} f(0)&=27 - 3\cdot 0 = 27;& \\ f(3)&=27 - 3\cdot 3 = 18.& \end{aligned}\] Le segment représentant $f$ est donc le segment [MN] avec M(0;27) et N(3;18).
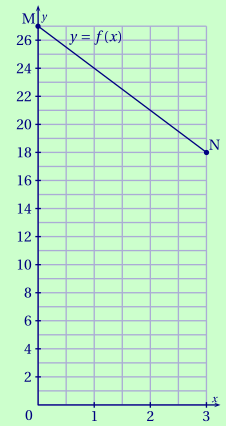
-
Par lecture directe du graphique, répondre aux questions suivantes :
-
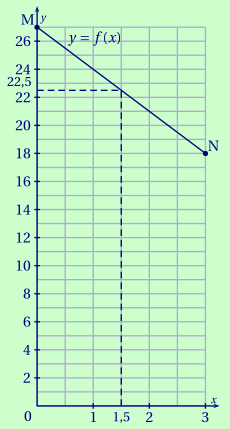
quelle est la valeur de $x$ pour laquelle le volume $f(x)$ est égal à $22,5$ cm3 ?
CorrigéLe point de [MN] d'ordonnée 22,5 a pour abscisse 1,5. Donc \[f(1,5)=22,5.\]
-
quel est le volume correspondant à $\mathrm{DK}= 2,5$ cm ?
CorrigéLe point de [MN] d'abscisse 2,5 a pour ordonnée 19,5. Donc \[f(2,5) = 19,5.\]
-
quelle est la valeur de $x$ pour laquelle le volume $f(x)$ est égal à $22,5$ cm3 ?
retour
code : 387