EX-05

retour

Dans la figure ci-dessous, une coccinelle part de S et se déplace sur les chemins de la figure ci-contre, délimités par les points A, B, C, D, E et S.

La coccinelle met une minute pour parcourir chaque segment, quelle que soit sa longueur.

Chaque fois qu'il arrive en un point, il choisit de manière équiprobable un chemin au hasard (et peut donc éventuellement rebrousser chemin).

On note :

C l'événement « le trajet du scarabée passe par le point C »;
D l'événement « le trajet du scarabée passe par le point D ».

1. Dans cette question, la coccinelle se déplace pendant 3 minutes.

a. Construire un arbre qui décrit tous les trajets de 3 minutes possibles.
Corrigé

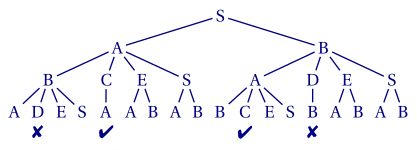
b. Déterminer P(C) et P(C∪ D).
Corrigé

Il y a 18 parcours possibles pour la coccinelle, parmi lesquels 2 passent par le point C (marque ✓ sur l'arbre).
Donc \[P(C) = \dfrac{2}{18}=\dfrac{1}{9}.\] On a marqué par ✖ les parcours passant par le point D.
Il y a donc 4 parcours qui passent par C ou D : \[P(C\cup D) = \dfrac 4 {18} = \dfrac 2 9.\]

2. Quelle doit être la durée minimale de parcours du scarabée pour que les événements C et D cessent d'être incompatibles ?
Corrigé

Pour que C et D ne soient pas incompatibles, il faut et suffit que l'on puisse réaliser un parcours contenant à la fois C et D.
On ne peut pas faire plus court que SACABD ou SBDBAC.
Le parcours du scarabée doit donc durer au moins 5 minutes.

3. La cocinnelle se déplace pendant 10 minutes. Une simulation informatique a permis d'obtenir les résultats suivants :

Nombre total de parcours: 26 098 ;
Nombre de parcours passant par C : 7202 ;
Nombre de parcours passant par D : 7202 ;
Nombre de parcours passant par C et D : 1154.

Déterminer P(C) puis P(C∪D) (on arrondira le résultat final à 10⁻²).
Corrigé

\[\begin{aligned} P(C) &= \dfrac{7202}{26098} \approx 0,28.& \\ P(C\cup D) &= P(C) + P(D) - P(C\cap D) \\ &= \dfrac{7202}{26098}+\dfrac{7202}{26098} -\dfrac{1154}{26098}& \\ &= \dfrac{13250}{26098} \approx 0,51.& \end{aligned}\]

retour

code : 333