retour

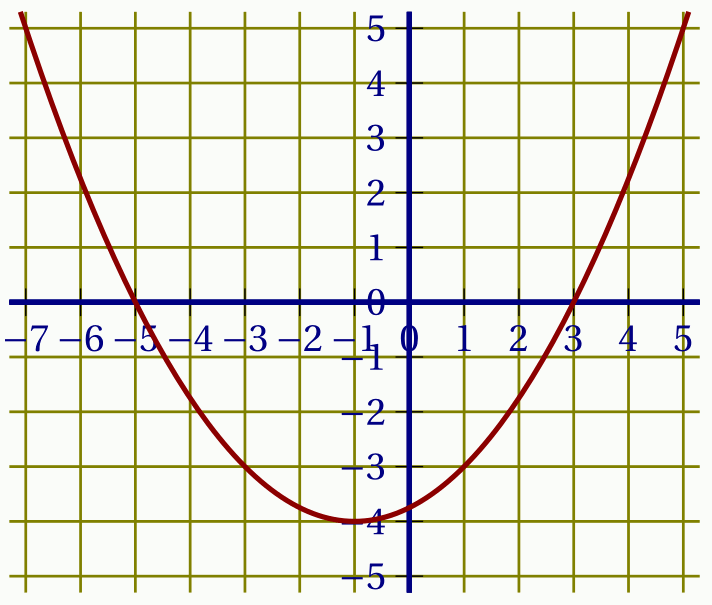
$f$ est la fonction définie sur $\mathbb R$ dont une représentation graphique $\mathscr C_f$ est donnée ci-dessous.

Elle est dérivable sur $\mathbb R$.

1. Résoudre dans $\mathbb R$, sans justifier, les inéquations :
   1. $f(x) \leqslant 0$; Corrigé
      $f(x) \leqslant 0$ quand la courbe de $f$ se situe sous l'axe des abscisses : \[S = [-5;3].\]
   2. $f'(x) \leqslant 0$. Corrigé
      $f'(x) \leqslant 0$ quand la fonction $f$ est décroissante : \[S=]-\infty;-1].\]
2. On sait de plus que  :
   $f'(-3) = -1$, $f'(-1) = 0$ et $f'(3) = 2$.
   Reproduire le graphique ci-dessus et tracer :
   1. La tangente $T_{-3}$ à $\mathscr C_f$ au point d'abscisse $-3$.
   2. La tangente $T_{-1}$ à $\mathscr C_f$ au point d'abscisse $-1$.
   3. La tangente $T_{3}$ à $\mathscr C_f$ au point d'abscisse 3.
   
   Corrigé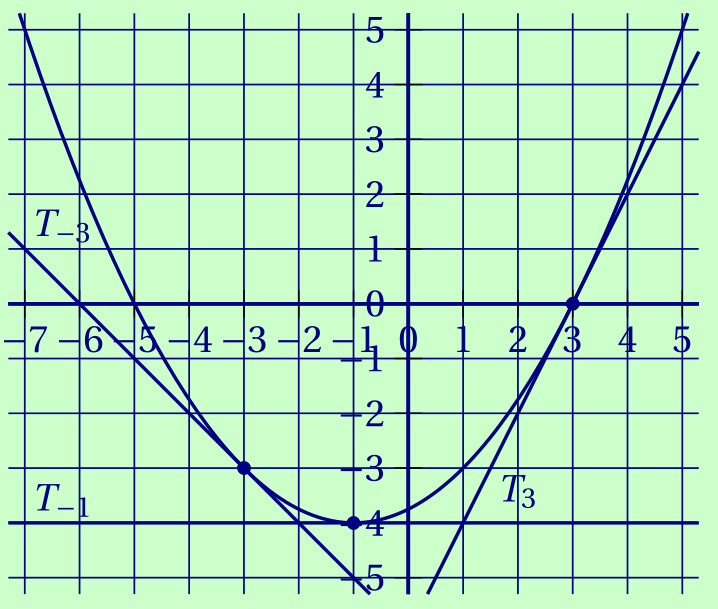
   

retour

code : 332