ex-2970 - Probas et suites
retour
Un étudiant mange tous les jours au restaurant universitaire. Ce restaurant propose des plats végétariens et des plats non végétariens.
- Lorsqu'un jour donné l'étudiant a choisi un plat végétarien, la probabilité qu'il choisisse un plat végétarien le lendemain est 0,9.
- Lorsqu'un jour donné l'étudiant a choisi un plat non végétarien, la probabilité qu'il choisisse un plat végétarien le lendemain est 0,7.
Le jour de la rentrée, l'étudiant a choisi le plat végétarien. On a donc $p_1 = 1$.
1.a. Indiquer la valeur de $p_2$.
Puisque l'on sait que $V_1$ est réalisé, alors $P(V_2) = P_{V_1}(V_2) = 0,9$.
b. Montrer que $p_3 = 0,88$. On pourra s'aider d'un arbre pondéré.
On peut proposer l'arbre pondéré suivant:
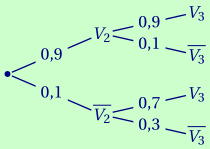
On cherche $p_3 = P(V_3)$. Or selon la formule des probabilités totales: \[\begin{aligned} P(V_3) &= P(V_3\cap V_2) + P(V_3 \cap \overline{V_2})& \\ &=P(V_2)\times P_{V_2}(V_3) + P(\overline{V_2})\times P_{\overline{V_2}}(V_3)& \\ &=0,9 \times 0,9 + 0,1\times 0,7& \\ &=0,88.& \end{aligned}\]
c.
Sachant que le 3e jour l'étudiant a choisi un plat végétarien,
quelle est la probabilité qu’il ait choisi un plat non végétarien le jour précédent ?
On arrondira le résultat à 10−2.
2.
Recopier et compléter l'arbre pondéré ci-dessous :
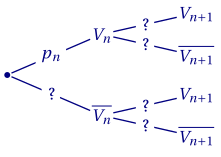
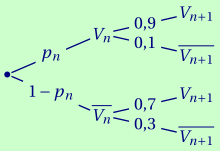
3. Justifier que, pour tout entier naturel $n \geqslant 1$, $p_{n+1} = 0,2p_n + 0,7$.
4.
On souhaite disposer de la liste des premiers termes de la suite $(p_n)$ pour $n \geqslant 1$.
Pour cela, on utilise une fonction appelée
repas programmée en langage Python dont on propose trois versions,
indiquées ci-dessous.

Programme 2 :

Programme 3 :

a.
Lequel de ces programmes permet d’afficher les $n$ premiers termes de la suite $(p_n)$?
Aucune justification n'est attendue.
b. Avec le programme choisi à la question a. donner le résultat affiché pour $n = 5$.
5. Démontrer par récurrence que, pour tout naturel $n \geqslant 1$, \[p_n = 0,125 \times 0,2^{n - 1} + 0,875.\]
Initialisation : Si $n = 1$, \[\begin{aligned} &0,125\times 0,2^{n-1} + 0,875& \\ &= 0,125\times 0,2^0 + 0,875& \\ &= 0,125\times 1 + 0,875& \\ &= 1.& \end{aligned}\] Or $p_1 = 1$. Donc $\mathscr A(1)$ est vraie.
Hérédité. Supposons que pour un entier naturel $k$ non nul quelconque, $\mathscr A(k)$ soit vraie.
Donc on suppose que $p_k = 0,125\times 0,2^{k-1} + 0,875$.
Alors: \[\begin{aligned} p_{k+1} &= 0,2 p_n + 0,7 = 0,2(0,125\times 0,2^{k-1} + 0,875) + 0,7& \\ &=0,125 \times 0,2\times 0,2^{k-1} + 0,2\times 0,875 + 0,7& \\ &=0,125 \times 0,2^{k+1-1} + 0,175 + 0,7& \\ &=0,125 \times 0,2^{(k+1) - 1} + 0,875.& \end{aligned}\] Donc $\mathscr A(k+1)$ est alors aussi vraie.
Initialisée et héréditaire, l'assertion $\mathscr A(n)$ est donc vraie par récurrence pour tout entier naturel $n$ non nul.
6. En déduire la limite de la suite $(p_n)$.
Donc, par produit puis somme: $\displaystyle\lim_{n\to+\infty} 0,125\times 0,2^{n-1} + 0,875 = 0,875$.
retour
code : 2970