ex-2964 - QCM fonctions
retour
Cet exercice est un QCM. Pour chaque question, une seule des réponses proposées est exacte.
1.
Soit $f$ la fonction définie sur $\mathbb R$ par $f(x) = \mathrm{e}^{-x^2+1}$.
La fonction $f$ admet pour dérivée la fonction $f'$ définie sur $\mathbb R$ par:
- $f'(x) = \mathrm{e}^{-x^2+1}$;
- $f'(x) = \left(-x^2 +1\right)\mathrm{e}^{-x^2+1}$;
- $f'(x) = - 2x\mathrm e^{-x^2+1}$;
- $f'(x) = \mathrm{e}^{-2x}$.
2.
Soit $a$ un réel quelconque. On pose :
$B = \dfrac{\mathrm e^{a}\times \mathrm e^{3-a}}{\mathrm e}$.
Alors :
- $B = \mathrm e^2$;
- $B = 7,39$;
- $B = \mathrm e^{3a-a^2-1}$;
- $B = a \times \mathrm e^{3-a}$.
Pour les deux questions suivantes, on a représenté ci-dessous la courbe représentative d'une fonction $f$ ainsi que deux de ses tangentes aux points d'abscisses respectives 2 et 4.
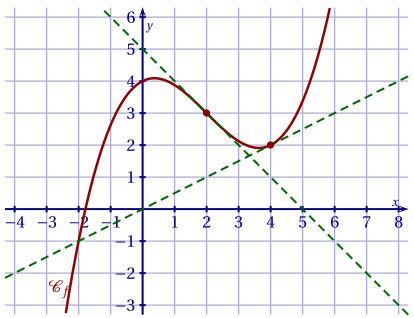
3. $f'(4)$ est égal à:
- $2$;
- $-1$;
- $0,5$;
- $0$.
Elle a donc pour coefficient directeur $\dfrac{2-0}{4-0} = \dfrac12 = 0,5$.
4. $f$ est convexe sur l'intervalle:
- ]−∞ ; 2];
- ]−∞ ; 0,5];
- [0 ; 4];
- [2 ; 5].
5.
Soit la fonction $f$ définie sur l'intervalle $[-10;10]$ par $f(x) = (2x - 3)\mathrm{e}^{-3x}$.
L'équation $f(x) = 0$ admet sur l'intervalle $[-10;10]$:
- 0 solution;
- 1 solution;
- 2 solutions;
- 3 solutions ou plus.
6.
Soit $g$ la fonction définie sur $[-1\;;\;4]$ par $g(x) = - x^3 + 3x^2 - 1$
et $\mathcal{C}_g$ sa courbe représentative dans un repère.
La tangente à la courbe $\mathcal{C}_g$ au point d'abscisse 1 a pour équation:
- $y = - 3x^2 + 6x$;
- $y= 3x-2$;
- $y= 3x - 3$;
- $y = 2x - 1$.
D'autre part $g$ est dérivable sur $[-1\;;\;4]$ et \[g'(x) =-3x^2 + 3\times 2x - 0 = -3x^2 + 6x.\] Donc \[g'(1) = -3\times 1^2 + 6\times 1 = -3+6 = 3.\] L'équation de la tangente est donc: \[y = 3(x - 1) + 1 \iff y = 3x - 2.\]
Pour les trois questions suivantes, on considère la fonction $f$ définie et dérivable sur $\mathbb R$ dont la courbe représentative $\mathcal{C}_f$ est donnée ci-dessous.
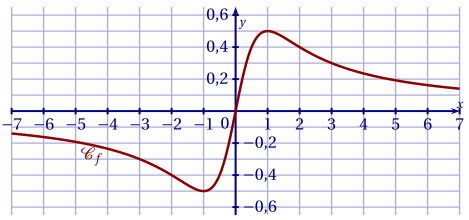
7. Le nombre de solutions dans $[-7;7]$ de l'équation $f'(x) = 0$ est :
- 0;
- 1;
- 2;
- 3.
8. Une valeur approchée de la solution de l'équation $f(x) = - 0,3$ sur l'intervalle $[-1;6]$ est:
- −3;
- −0,3;
- 0,3;
- 3.
9. Le nombre de points d'inflexion dans [−7;7] de $\mathcal{C}_f$ est:
- 0;
- 1;
- 2;
- 3.
Il y a donc deux changements de concavité donc deux points d'inflexion.
retour
code : 2964