295
retour
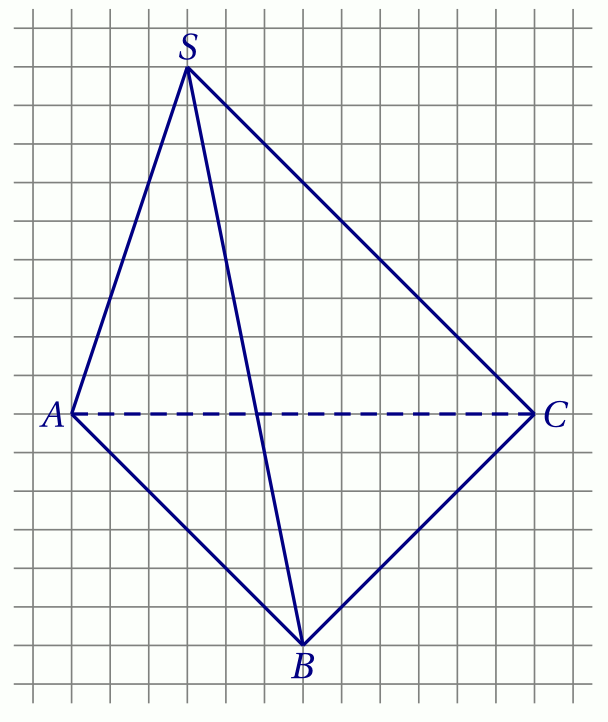
On considère le tétraèdre $SABC$ ci-dessous.
-
Reproduire la figure et placer les points $M$, $N$ et $P$ tels que :
\[\overrightarrow{AM} = \frac 3 2 \overrightarrow{AB};\qquad
\overrightarrow{BN} = 2\overrightarrow{BA}\quad
\overrightarrow{AP} = -\frac 2 3 \overrightarrow{AS}.\]
Corrigé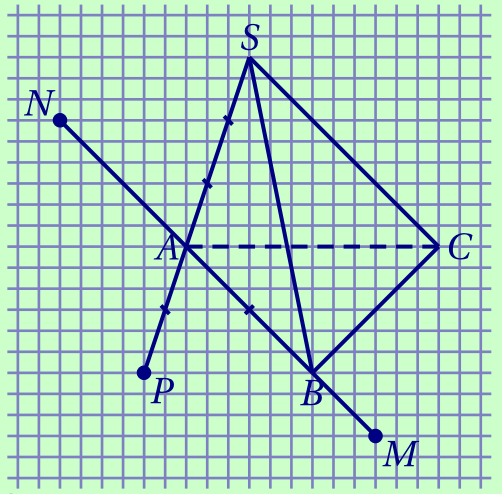
- Exprimer le vecteur $\overrightarrow{SM}$ en fonction des vecteurs $\overrightarrow{SA}$ et $\overrightarrow{SB}$.
CorrigéOn a: \begin{align*} \overrightarrow{SM} &=\overrightarrow{SA}+\overrightarrow{AM}& \\ &=\overrightarrow{SA}+\frac 3 2 \overrightarrow{AB}& \\ &=\overrightarrow{SA} + \frac 3 2 \left(\overrightarrow{AS}+\overrightarrow{SB}\right)& \\ &=\overrightarrow{SA}+\frac 3 2 \overrightarrow{AS} + \frac 3 2 \overrightarrow{SB}& \\ &=\overrightarrow{SA}- \frac 3 2 \overrightarrow{SA} + \frac 3 2\overrightarrow{SB}& \\ &=-\frac 1 2 \overrightarrow{SA} + \frac 3 2 \overrightarrow{SB}.& \end{align*}- Exprimer de même le vecteur $\overrightarrow{NP}$ en fonction des vecteurs $\overrightarrow{SA}$ et $\overrightarrow{SB}$.
CorrigéDe même: \begin{align*} \overrightarrow{NP} &=\overrightarrow{NB} + \overrightarrow{BA} + \overrightarrow{AP}& \\ &=-2\overrightarrow{BA} + \overrightarrow{BA} - \frac 2 3 \overrightarrow{AS}& \\ &=-\overrightarrow{BA} + \frac 2 3 \overrightarrow{SA}& \\ &=-\overrightarrow{BS} - \overrightarrow{SA} + \frac 2 3 \overrightarrow{SA}& \\ &=\overrightarrow{SB} - \frac 1 3 \overrightarrow{SA}& \\ &=-\frac 1 3 \overrightarrow{SA} + \overrightarrow{SB}.& \end{align*}- Montrer que les droites $(SM)$ et $(NP)$ sont parallèles.
CorrigéOn peut remarquer que: \[\begin{aligned} \frac 3 2 \overrightarrow{NP} &= \frac 3 2 \left(-\frac 1 3 \overrightarrow{SA}+\overrightarrow{SB}\right)& \\ &=-\frac 1 2 \overrightarrow{SA} + \frac 3 2 \overrightarrow{SB}& \\ &=\overrightarrow{SM}.& \end{aligned}\] Les vecteurs $\overrightarrow{NP}$ et $\overrightarrow{SM}$ sont colinéaires, donc les droites $(NP)$ et $(SM)$ sont parallèles.retour
code : 295
- Exprimer le vecteur $\overrightarrow{SM}$ en fonction des vecteurs $\overrightarrow{SA}$ et $\overrightarrow{SB}$.