retour

Partie A

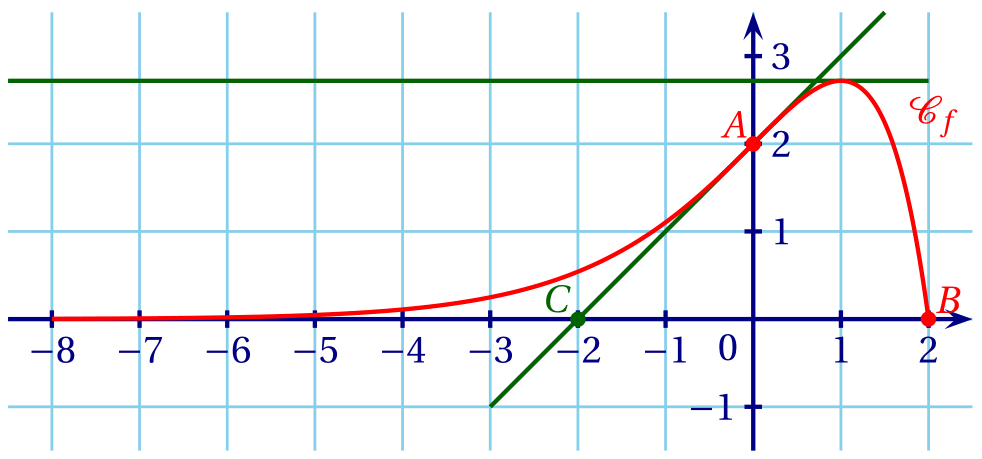
Dans le repère ci-dessous, on note $\mathcal{C}_f$ la courbe représentative d'une fonction $f$ définie sur l'intervalle $[-8;2]$.
On a placé les points $A(0;2)$, $B(2;0)$ et $C(-2;0)$.

On dispose des renseignements suivants :

• Le point $B$ appartient à la courbe $\mathcal{C}_f$.
• La droite $(AC)$ est tangente en $A$ à la courbe $\mathcal{C}_f$.
• La tangente à la courbe $\mathcal{C}_f$ au point d'abscisse 1 est une droite horizontale.

Répondre aux questions suivantes par lecture graphique.

1. Indiquer les valeurs de $f(0)$ et de $f(2)$.
   Corrigé
   Puisque $A(0\;;\;2)\in\mathscr C_f$, $f(0) = 2$.
   Puisque $B(2\;;\;0)\in\mathscr C_f$, $f(2) = 0$.
2. Indiquer la valeur de $f'(1)$.
   Corrigé
   La tangente à $\mathscr C_f$ au point d'abscisse 1 est horizontale et admet donc un coefficient directeur nul.
   Donc \[f'(1) = 0.\]
3. Donner une équation de la tangente à la courbe $\mathcal{C}_f$ au point $A$.
   Corrigé
   La droite $(AC)$ admet pour coefficient directeur $\dfrac{2}{2} = 1$ et elle coupe l'axe des ordonnées au point d'ordonnée 2.
   Son équation affine est donc \[y = x + 2.\]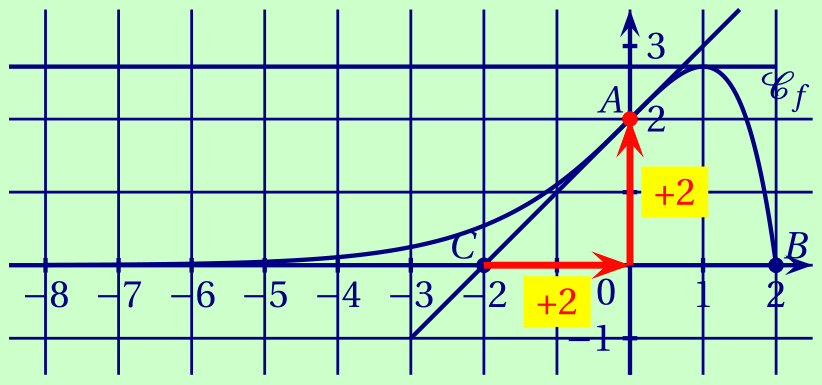

   
4. Indiquer le nombre de solutions de l'équation $f(x) = 1$ dans l'intervalle $[-8;2]$.
   Corrigé
   Deux points de $\mathscr C_f$ ont pour ordonnée 1. Donc l'équation $f(x) = 1$ doit avoir deux solutions.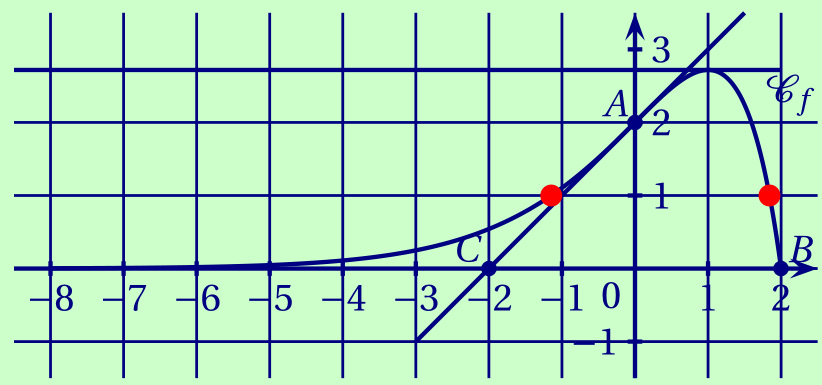

   
5. Indiquer les variations de la fonction $f$ sur l'intervalle $[-8;2]$.
   Corrigé
   La fonction $f$ semble croissante sur $[-8\;;\;1]$ et décroissante sur $[1\;;\;2]$.
6. Déterminer l'intervalle sur lequel la fonction $f$ est convexe, et celui sur lequel elle est concave.
   Corrigé
   $f$ semble convexe sur $[-8;0]$ et concave sur $[0;2]$. D'ailleurs, la courbe $\mathscr C_f$ étant traversée par sa tangente en $A$, $A$ semble bien être un point d'inflexion.

Partie B

Dans cette partie, on cherche à vérifier par le calcul les résultats lus graphiquement dans la partie A.

On sait désormais que la fonction $f$ est définie sur l'intervalle $[-8;2]$ par: \[f(x) = (2 - x)\mathrm{e}^x.\]

1. Calculer $f(0)$, $f(1)$ et $f(2)$.
   Corrigé
   \[\begin{aligned} f(0) &= (2-0)\mathrm e^0 = 2\times 1 = 2\;;& \\ f(1) &=(2-1)\mathrm e^1 = 1\times \mathrm e = \mathrm e\;;& \\ f(2) &=(2-2)\mathrm e^2 = 0 \times \mathrm e^2 = 0.& \end{aligned}\]
2. 1. Calculer $f'(x)$ pour tout nombre $x$ appartenant à l'intervalle $[-8;2]$.
      Corrigé
      $f=u\times v$ où $u(x) = 2 - x$ et $v(x) = \mathrm e^x$. $u$ et $v$ sont dérivables sur $[-8;2]$, donc $f$ aussi et \[\begin{aligned} f'(x) &= u'(x)\cdot v(x) + u(x) \cdot v'(x)& \\ &= -1\mathrm e^x + (2-x)\mathrm e^x& \\ &=(-1+2-x)\mathrm e^x& \\ &=(1-x)\mathrm e^x.& \end{aligned}\]
   2. En déduire la valeur de $f'(1)$.
      Corrigé
      On en déduit que \[f'(1) = (1-1)\mathrm e^1 = 0 \times \mathrm e = 0.\]
3. Déterminer une équation de la tangente à la courbe représentative de $f$ au point d'abscisse $0$.
   Corrigé
   Nous avons \[f'(0) = (1-0)\mathrm e^0 = 1\times 1 = 1.\] L'équation de la tangente à $\mathscr C_f$ en $0$ est donc \[\begin{aligned} y &= f'(0)(x-0) + f(0)& \\ \iff y &= 1(x - 0) + 2& \\ \iff y &=x + 2.& \end{aligned}\]
4. 1. Dresser le tableau des variations de la fonction $f$ sur l'intervalle $[-8;2]$.
      Corrigé
      Puisque l'exponentielle est strictement positive, le signe de $f'(x)$ est aussi celui de $1-x$.\\ On peut donc dresser le tableau de variations suivant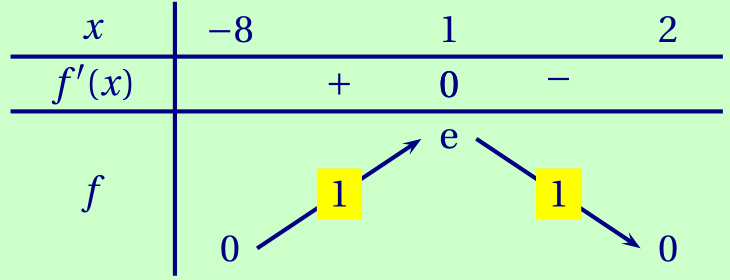

      
   2. En déduire le nombre de solutions de l'équation $f(x) = 1$ dans l'intervalle $[-8;2]$, puis donner une valeur approchée au centième de chacune de ces solutions.
      Corrigé
      Puisque $0 < 1 < \mathrm e$, le tableau de variation nous permet d'affirmer que l'équation $f(x) = 1$ admet deux solutions.
      Une recherche heuristique (par exemple avec la fonction "table" d'une calculatrice) permet d'obtenir que \[\begin{aligned} f(-1,147) &\approx 0,999\;;& \\ f(-1,146) &\approx 1,0001.& \end{aligned}\] Donc une solution appartient à l'intervalle $[-1,147\;;\;-1,146]$, sa valeur arrondie au centième étant donc $-1,15$.
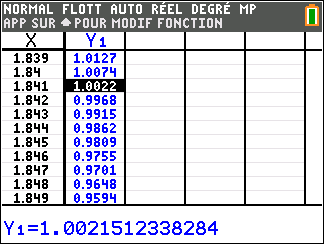
      On trouve de même que: \[\begin{aligned} f(1,841) &\approx 1,002\;;& \\ f(1,842)&\approx 0,997.& \end{aligned}\] La deuxième solution appartient donc à l'intervalle $[1,841\;;\;1,842]$, ce qui signifie que sa valeur arrondie au centième est $1,84$.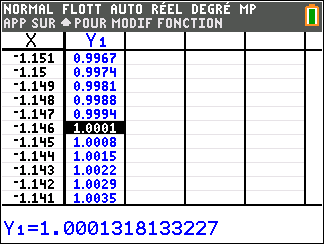

      
      
5. Retrouver par le calcul l'intervalle sur lequel la fonction $f$ est convexe.
   Corrigé
   La fonction $f'$ est de la forme $f'=u\times v$ avec $u(x) = 1- x$ et $v(x) =\mathrm e^x$.
   Ces deux fonctions étant dérivables sur $[-8\;;\;2]$, $f'$ l'est aussi et \[\begin{aligned} f''(x) &= u'(x)\cdot v(x) + u(x)\cdot v'(x)& \\ &=-1\times \mathrm e^x + (1-x)\mathrm e^x& \\ &=(-1 + 1 - x)\mathrm e^x& \\ &=-x\mathrm e^x.& \end{aligned}\] L'exponentielle étant strictement positive, $f''(x)$ est du signe de $-x$, donc positive sur l'intervalle $[-8;0]$.
   C'est donc sur cet intervalle que la fonction $f$ est convexe.

retour

code : 243