EX-72

retour

On considère la suite $\left(u_{n}\right)$ définie par $u_{0} = 0$ et, pour tout entier naturel $n$ \[u_{n+1} = u_{n} + 2n + 2.\]

1. Calculer $u_{1}$ et $u_{2}$.
Corrigé

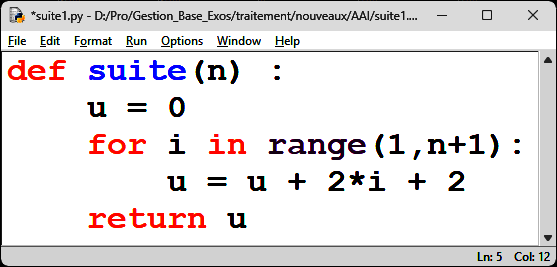
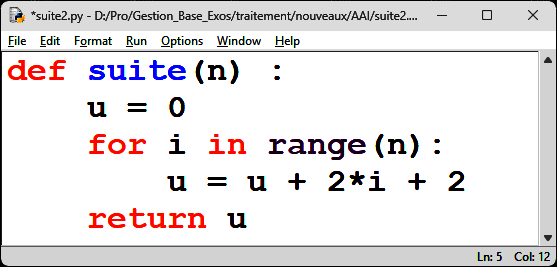
\[\begin{aligned} u_1 &=u_0 + 2\times 0 + 2 = 0+0+2 = 2\ ;&\\ u_2 &=u_1 + 2\times 1 + 2 = 2 + 2 + 2 = 6.& \end{aligned}\]

2. On considère les deux fonctions programmées en Python suivantes

Fonction 1 Fonction 2
De ces deux fonctions, laquelle permet d'afficher en sortie la valeur de $u_{n}$, la valeur de l'entier naturel $n$ étant en paramètre de la fonction ?
Corrigé
C'est la fonction 2. La valeur de l'indice i dans la fonction 1 n'est pas correct.
En fait, la fonction 1 calcule les termes d'une suite qui vérifierait \[u_{n+1} = u_n + 2(n+1) + 2.\]

3. À l'aide d'un tableur, on a obtenu le tableau et le nuage de points ci-dessous où $n$ figure en abscisse et $u_{n}$ en ordonnée.

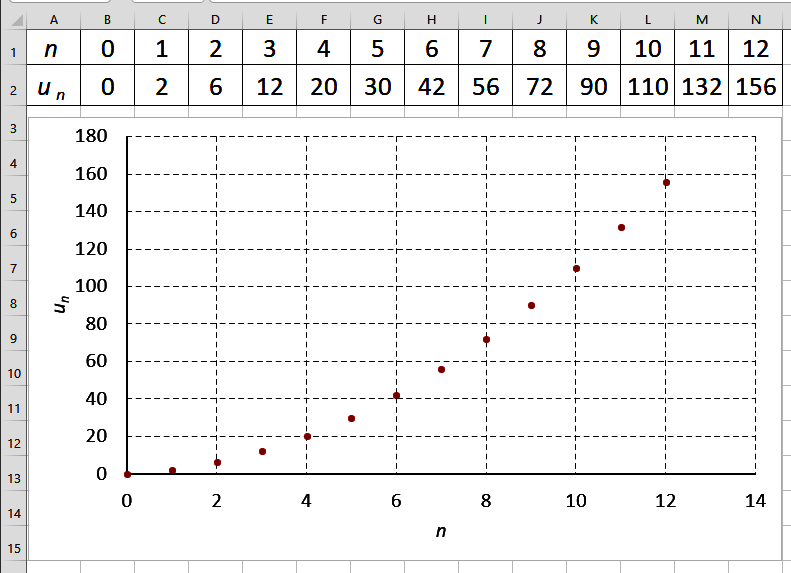
a. Quelle conjecture peut-on faire quant au sens de variation de la suite $\left(u_{n}\right)$ ?

Corrigé

$(u_n)$ semble croissante.
Démontrer cette conjecture.
Corrigé
Pour tout entier naturel $n$: \[u_{n+1} - u_n = u_n + 2n + 2 - u_n = 2n + 2.\] Or \[n \ge 0 \implies 2n + 2 \ge 2 \implies 2n+2 > 0.\] La suite $(u_n)$ est donc bien strictement croissante.

b. La forme parabolique du nuage de points amène à conjecturer l'existence de trois réels a, b et c tels que, pour tout entier naturel n, \[u_{n} = an^2 + bn + c.\]
Dans le cadre de cette conjecture, trouver les valeurs de a, b et c à l'aide des informations fournies.
Corrigé

Si $u_n = an^2 + bn + c$, alors en particulier on a: \[u_0 = a\times 0^2 + b\times 0 + c = 0.\] Donc $c = 0$.
On aura aussi \[ u_1 = 2 \implies a\times 1^2 + b\times 1 = 2 \implies b = 2 - a. \] Enfin, on aura \[\begin{aligned} &u_2 = 6& \\ \implies &a\times 2^2 + b\times 2 = 6& \\ \implies &4a + 2b = 6& \\ \implies &2a + b = 3& \\ \implies &2a + 2 - a = 3& \\ \implies &a = 1.& \end{aligned}\] Ce qui implique alors que \[b = 2 - a = 2 - 1 = 1.\] Si $u_n =an^2+bn + c$, alors $a=b=1$ et $c=0$.

4. On définit, pour tout entier naturel $n$, la suite $\left(v_{n}\right)$ par : \[v_{n} = u_{n+1} - u_{n}.\]

a. Exprimer $v_{n}$ en fonction de l'entier naturel $n$.
Corrigé

On a déjà vu à la question 3.a que \[v_{n} = u_{n+1} - u_n = 2n +2.\]

Quelle est la nature de la suite $\left(v_{n}\right)$ ?
Corrigé
On reconnaît là l'expression en fonction de $n$ de la suite arithmétique de raison $2$ et premier terme $v_0 = 2$.

b. On définit, pour tout entier naturel $n$, \[S_{n} = \sum_{k=0}^{n} v_{k} = v_{0} + v_{1} + \cdots + v_{n}.\] Démontrer que, pour tout entier naturel $n$, \[S_{n} = (n + 1)(n + 2).\] Corrigé

\[\begin{aligned} S_n & = v_0 + v_1 + v_2 + \cdots + v_n&\\ & = (2\times 0 + 2) + (2\times 1 + 2) + (2\times 2 + 2) + \cdots + (2n + 2)& \\ & = 2\times 0 + 2\times 1 + 2\times 2 + \cdots + 2n + \underbrace{2+2+2+\cdots+2}_{(n+1)\times 2}& \\ & = 2(0+1+2+\cdots+n) + 2(n+1)& \\ & = 2\times \frac{n(n+1)} 2 + 2(n+1)& \\ & = n(n+1) + 2(n+1)& \\ &=(n+1)(n+2). \end{aligned}\]

c. Démontrer que, pour tout entier naturel $n$, \[S_{n} = u_{n+1} - u_{0}.\] Corrigé

\[\begin{aligned} S_n &= v_0 + v_1 + v_2 + \cdots + v_n& \\ &=\cancel{u_1} - u_0 + \cancel{u_2} - \cancel{u_1} + \cancel{u_3} - \cancel{u_2} + \cdots + u_{n+1} - \cancel{u_n}& \\ &=u_{n+1} - u_0.& \end{aligned}\]

d. Exprimer $u_{n}$ en fonction de $n$.
Corrigé

D'après les deux formules précédentes, on peut écrire que: \[S_{n-1} = u_{n} - u_0 = n(n+1).\] On a donc : \[u_{n} - u_0 = n(n+1) \implies u_n = n^2 + n + u_0 = n^2 + n.\]

retour

code : 235