retour

Pour assurer la souveraineté de sa famille, un roi se doit d'avoir un fils pour lui succéder à sa mort.
On suppose que pour chaque naissance d'un enfant d'un roi et d'une reine donnés, la probabilité que ce soit un garçon est 0,3.
On suppose que les naissances sont indépendantes.

1. Le roi et la reine ont trois enfants. Quelle est la probabilité
   1. qu'ils n'aient aucun garçon ?
      Corrigé
      On peut modéliser la situation à l'aide de l'arbre suivant ( où $G$ désigne "garçon" et $F$ désigne "fille").

      

      Probabilité d'avoir 3 filles (donc aucun garçon): \[0,7^3 = 0,343.\]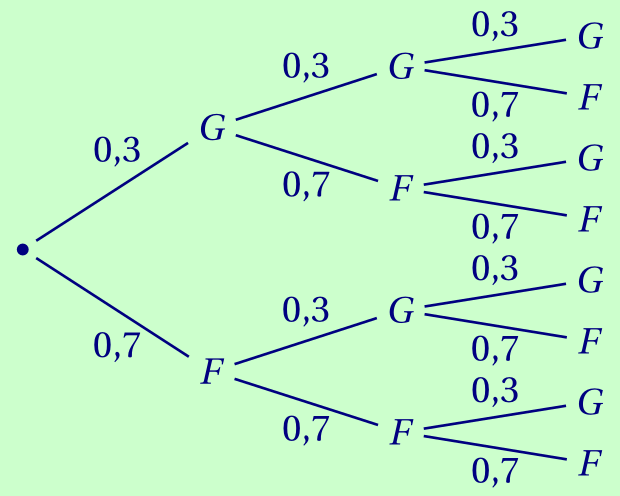
   2. qu'ils aient au moins un garçon ?
      Corrigé
      C'est l'événement contraire de l'événement précédent, donc sa probabilité est : \[1-0,343 = 0,657.\]
2. On suppose que le couple met au monde $n$ enfants, avec $n$ un entier naturel non nul.
   1. Exprimer, en fonction de $n$, la probabilité que le roi et la reine aient au moins un garçon.
      Corrigé
      La probabilité de n'avoir aucun garçon est \[0,7^n.\] Donc la probabilité d'en avoir au moins un est \[1 - 0,7^n.\]
   2. On fait tourner le programme Python suivant:
      n = 0 while 1-0.7**n < 0.99 : n = n + 1 print(n)
      Le programme affiche le nombre 13. Quelle est la signification de ce nombre ?
      Corrigé
      La boucle while calcule à chaque étape $1-0,7^n$ : c'est la probabilité d'avoir au moins un garçon parmi $n$ enfants.
      La boucle se poursuit tant que cette probabilité reste inférieure à 0,99. Donc quand la boucle s'arrête, la probabilité d'avoir au moins un garçon a égalé ou dépassé 0,99 pour la première fois.
      On affiche finalement $n$, soit le d'enfants mis au monde.
      Le programme affiche donc le nombre minimal d'enfant à mettre au monde si l'on veut que la probabilité d'avoir un garçon soit au moins égale à 99%.

retour

code : 145