retour

Lors d'une soirée, une chaîne de télévision a retransmis un match. Cette chaîne a ensuite proposé une émission d'analyse de ce match.

On dispose des informations suivantes :

• 56% des téléspectateurs ont regardé le match ;
• un quart des téléspectateurs ayant regardé le match ont aussi regardé l'émission ;
• 16,2% des téléspectateurs ont regardé l'émission.

On interroge au hasard un téléspectateur. On note les évènements :

• $M$ : « le téléspectateur a regardé le match » ;
• $E$ : « le téléspectateur a regardé l'émission ».

On note $x$ la probabilité qu'un téléspectateur ait regardé l'émission sachant qu'il n'a pas regardé le match.

1. Construire un arbre pondéré illustrant la situation.
   Corrigé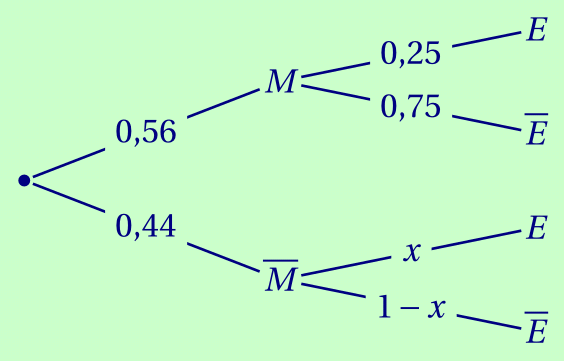
   
2. Déterminer la probabilité de $M \cap E$.
   Corrigé
   \[P(M\cap E) = P(M)\times P_M(E) =0,56\times 0,25 =0,14.\]
3. 1. Vérifier que $p(E) = 0,44x + 0,14$.
      Corrigé
      Selon la loi des probabilités totales: \[ \begin{aligned} P(E) &= P(M\cap E) + P(\overline M \cap E)& \\ &=0,14 + P(\overline M) \times P_{\overline M}(E)& \\ &=0,14 + 0,44x.& \end{aligned} \]
   2. En déduire la valeur de $x$.
      Corrigé
      Selon l'énoncé, $P(E) = 0,162$ donc: \[\begin{aligned} 0,44x + 0,14 &= 0,162& \\ \iff 0,44x &=0,162 - 0,14& \\ \iff x&=\frac{0,022}{0,44}& \\ \iff x&=0,05.& \end{aligned}\] Donc 5% des personnes n'ayant pas regardé le match ont cependant suivi l'émission.
4. Le téléspectateur interrogé n'a pas regardé l'émission. Quelle est la probabilité, arrondie à 10⁻², qu'il ait regardé le match ?
   Corrigé
   On cherche ici : \[ \begin{aligned} P_{\overline E}(M) &=\frac{P(M\cap \overline E)}{P(\overline E)}& \\ &=\frac{P(M)\times P_M(\overline E)}{1-P(E)}& \\ &=\frac{0,56 \times 0,75}{1-0,162}& \\ &\approx 0,50.& \end{aligned} \] Environ 50% des personnes qui n'ont pas regardé l'émission n'ont pas non plus regardé le match.

retour

code : 13