retour

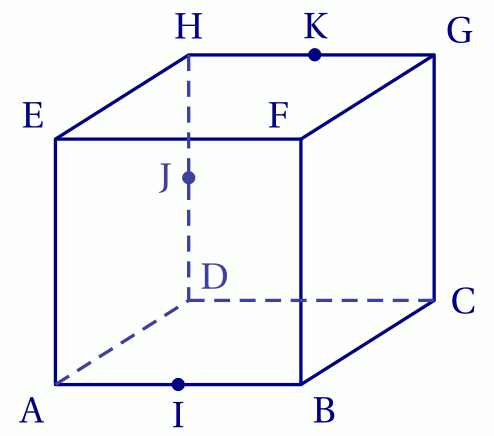
ABCDEFGH est un cube. I est le milieu de [AB], J est le milieu de [HD] et K est le milieu de [HG].

On se place dans le repère $(\mathrm{A}; \overrightarrow{\mathrm{AB}},\overrightarrow{\mathrm{AD}},\overrightarrow{\mathrm{AE}})$.

1. Démontrer que le vecteur $\overrightarrow{\mathrm{CE}}$ est un vecteur normal au plan (IJK).
   Corrigé
   On peut lire les coordonnées : \[\overrightarrow{\mathrm{IJ}}\begin{pmatrix}-1/2\\1\\1/2\end{pmatrix}, \ \overrightarrow{\mathrm{IK}}\begin{pmatrix}0\\1\\1\end{pmatrix}, \ \overrightarrow{\mathrm{CE}}\begin{pmatrix}-1\\-1\\1\end{pmatrix}.\] On en déduit que : \[\begin{aligned} &\overrightarrow{\mathrm{CE}}\cdot\overrightarrow{\mathrm{IJ}} =-\frac 1 2 \times (-1) + 1\times (-1) + \frac 1 2 \times 1 = 0& \\ &\overrightarrow{\mathrm{CE}}\cdot\overrightarrow{\mathrm{IK}} =-1\times 0 + 1\times (-1) + 1\times 1 = 0& \end{aligned}\] $\overrightarrow{\mathrm{CE}}$, orthogonal à la base $\left(\overrightarrow{\mathrm{IJ}},\overrightarrow{\mathrm{IK}}\right)$ du plan (IJK) est donc normal à ce plan.
2. Démontrer que la droite (BD) est parallèle au plan (IJK).
   Corrigé
   La droite (BD) sera parallèle au plan (IJK) si et seulement si les vecteurs $\overrightarrow{\mathrm{BD}}$, $\overrightarrow{\mathrm{IJ}}$ et $\overrightarrow{\mathrm{IK}}$ sont coplanaires.
   Supposons l'existence de deux réels $a$ et $b$ tels que \[\begin{aligned} &\overrightarrow{\mathrm{BD}} = a\overrightarrow{\mathrm{IJ}} + b\overrightarrow{\mathrm{IK}}& \\ \iff &\begin{cases} -1 = -\frac 1 2 a\\1 = a + b\\ 0 = \frac 1 2 a + b\end{cases}& \\ \iff &\begin{cases}\boxed{a = 2}\\b=1 - a\\b=-\frac 1 2 a\end{cases}& \\ \iff &\begin{cases}a = 2\\ b = 1 - 2 = -1\\b = -\frac 1 2 \times 2 = -1\end{cases}& \\ \iff &\overrightarrow{\mathrm{BD}} = 2\overrightarrow{\mathrm{IJ}} -\overrightarrow{\mathrm{IK}}& \end{aligned}\] Cette relation montre que les vecteurs $\overrightarrow{\mathrm{IJ}}$, $\overrightarrow{\mathrm{IK}}$ et $\overrightarrow{BD}$ sont coplanaires, donc que (BD) est parallèle au plan (IJK).
3. Soit M un point de la droite (CE). Quelle est la position du point M sur la droite (CE) pour laquelle le plan (BDM) est parallèle au plan (IJK) ?
   Corrigé
   On a déjà montré que la droite (BD) est parallèle au plan (IJK). Le plan (BDM) sera parallèle au plan (IJK) si et seulement si la droite (BM) est elle aussi parallèle au plan (IJK).
   On lit les coordonnées de B : B(1;0;0).
   $\overrightarrow{\mathrm{CE}}$ est un vecteur directeur de la droite (CE) et cette droite passe par le point E, donc une représentation paramétrique de la droite (CE) est \[\begin{cases}x = -t\\y = -t\\z=t+1\end{cases}.\] Puisque M est sur cette droite, il existe donc un réel $t$ tel que : \[x_M = -t,\quad y_M = -t,\quad z_M = t + 1.\] Donc le vecteur $\overrightarrow{\mathrm{BM}}$ a pour coordonnées \[\overrightarrow{\mathrm{BM}}\begin{pmatrix}x_M - x_B\\y_M - y_B\\z_M - z_B\end{pmatrix} \iff \overrightarrow{\mathrm{BM}}\begin{pmatrix}-t - 1\\-t\\t+1\end{pmatrix}\] La droite (BM) sera parallèle au plan (IJK) si et seulement s'il existe deux réels $a$ et $b$ tels que \begin{align*} &\overrightarrow{\mathrm{BM}} = a\overrightarrow{\mathrm{IJ}} + b\overrightarrow{\mathrm{IK}}& \\ \iff &\begin{cases} -t-1 = -\frac 1 2 a\\ -t = a + b\\ t+1 = \frac 1 2 a + b \end{cases}& \\ \iff &\begin{cases} \boxed{t = -1 + \frac 1 2 a}\\ 1 - \frac 1 2 a = a + b\\ \frac 1 2 a = \frac 1 2 a + b \end{cases}& \\ \iff &\begin{cases} t = -1 + \frac 1 2 a\\ 1 = \frac 3 2 a\\ \boxed{b = 0} \end{cases}& \\ \iff &\begin{cases} t = -1+\frac 1 2 \times \frac 2 3 = -\frac 2 3\\ \boxed{a = \frac 2 3}\\ b = 0 \end{cases}.& \end{align*} Donc finalement \[\left.\begin{array}{l} x_M = -t = \frac 2 3\\ y_M = -t = \frac 2 3\\ z_M = t+1 = \frac 1 3 \end{array}\right\} \implies M\left(\frac 2 3;\frac 2 3;\frac 1 3\right).\]

retour

code : 111