retour

Les interactions électriques conduisent à modéliser la molécule de méthane CH₄ de la façon suivante :

• Les noyaux d'atomes d'hydrogène occupent les positions des quatre sommets d'un tétraèdre régulier.
• Le noyau de carbone au centre de la molécule est à égale distance des quatre atomes d'hydrogène.

L'objectif est de déterminer une mesure de l'angle entre deux liaisons carbone-hydrogène.

Un tétraèdre régulier est un polyèdre dont les quatre faces sont des triangles équilatéraux.

1. Justifier qu'on peut inscrire ce tétraèdre dans un cube $ABCDEFGH$ en positionnant deux atomes d'hydrogène sur les sommets $A$ et $C$ du cube et les deux autres atomes d'hydrogène sur deux autres sommets du cube.
   Représenter la molécule dans le cube donné ci-après.
   
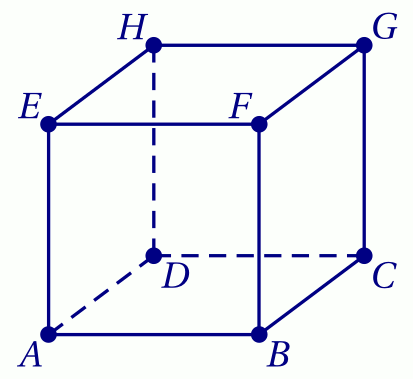
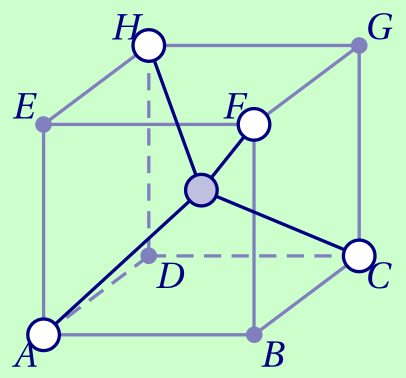
   Corrigé
   Les atomes d'hydrogène peuvent être représentés par les sommets $A$, $C$, $F$ et $H$.
   En effet, dans ce cas, les arêtes $[AF]$, $[AC]$, $[AH]$, $[CF]$, $[CH]$ et $[HF]$ sont toutes des diagonales de faces du cube, donc toutes de la même longueur.
   Par conséquent, le tétraèdre $ACFH$ est bien régulier.
   

Dans la suite de l'exercice, on pourra travailler dans le repère $(A;\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AE})$.

2. Démontrer que l'atome de carbone est au centre $\Omega$ du cube.
   Corrigé
   Il nous faut montrer que les distances de $\Omega$ au sommets $A$, $C$, $F$ et $H$ sont toutes égales.
   Or : \[\begin{aligned} &A(0;0;0);\quad &C(1;1;0);\quad &F(1;0;1); \\ &H(0;1;1)\quad& G(1;1;1).& \end{aligned}\] Du plus, $\Omega$, centre du cube, est le milieu de la diagonale $[AG]$. Donc : \[\left.\begin{array}{l} x_{\Omega} = \frac{x_A + x_G}2 = \frac{0+1} 2 = \frac 1 2 \\ y_{\Omega} = \frac{y_A + y_G}2 = \frac{0+1} 2 = \frac 1 2 \\ z_{\Omega} = \frac{z_A + z_G}2 = \frac{0+1} 2 = \frac 1 2. \end{array}\right\} \implies \Omega\left(\frac 1 2;\frac 1 2;\frac 1 2\right). \] Le vecteur $\overrightarrow{A\Omega}$ a pour coordonnées : \[\begin{pmatrix}x_{\Omega} - x_A \\ y_{\Omega} - y_A \\ z_{\Omega} - z_A \end{pmatrix} =\begin{pmatrix}\frac 1 2 - 0\\\frac 1 2 - 0\\\frac 1 2 - 0\end{pmatrix} =\begin{pmatrix}\frac 1 2\\\frac 1 2\\\frac 1 2\end{pmatrix} \] On en déduit que : \[\begin{aligned} A\Omega &= \lVert\overrightarrow{A\Omega}\rVert = \sqrt{\left(\frac 1 2\right)^2 + \left(\frac 1 2\right)^2 + \left(\frac 1 2\right)^2}& \\ &=\sqrt{\frac 3 4}& \\ &= \frac{\sqrt 3} 2.& \end{aligned}\] De manière analogue, on montre que \[\begin{aligned} &\overrightarrow{C\Omega}\begin{pmatrix}-1/2\\-1/2\\1/2\end{pmatrix} \implies C\Omega = \frac{\sqrt 3} 2\;;& \\ &\overrightarrow{F\Omega}\begin{pmatrix}-1/2\\1/2\\-1/2\end{pmatrix} \implies F\Omega = \frac{\sqrt 3}2\;;& \\ &\overrightarrow{H\Omega}\begin{pmatrix}-1/2\\1/2\\1/2\end{pmatrix} \implies H\Omega = \frac{\sqrt 3} 2.& \end{aligned}\] Puisque \[A\Omega = C\Omega = F\Omega = H\Omega,\] $\Omega$ est bien la position de l'atome de carbone.
3. Déterminer l'arrondi au dixième de degré de la mesure de l'angle que forment entre elles les liaisons carbone-hydrogène, c'est-à-dire l'angle $\widehat{A\Omega C}$.
   Corrigé
   On sait que : \[\begin{aligned} \overrightarrow{\Omega A} = -\overrightarrow{A\Omega} &\implies \overrightarrow{\Omega A}\begin{pmatrix}-1/2\\-1/2\\-1/2\end{pmatrix}\;;& \\ \overrightarrow{\Omega C} = -\overrightarrow{C\Omega} &\implies \overrightarrow{\Omega C}\begin{pmatrix}1/2\\1/2\\-1/2\end{pmatrix}.& \end{aligned}\] Donc : \begin{align*} \overrightarrow{\Omega A}\cdot\overrightarrow{\Omega C} &={\scriptsize \left(-\frac 1 2\right)\times\left(\frac 1 2\right) + \left(-\frac 1 2\right)\times \left(\frac 1 2\right) + \left(-\frac 1 2\right)\times\left(-\frac 1 2\right)}& \\ &=-\frac 1 4 - \frac 1 4 + \frac 1 4& \\ &= -\frac 1 4.& \end{align*} Mais d'autre part : \[\begin{aligned} \Omega A \times \Omega C \times \cos\widehat{A\Omega C} &= \overrightarrow{\Omega A}\cdot \overrightarrow{\Omega C}& \\ \iff \frac{\sqrt 3} 2 \times \frac{\sqrt 3} 2 \times \cos\widehat{A\Omega C} &= -\frac 1 4& \\ \iff \frac 3 4\cos\widehat{A\Omega C} &= -\frac 1 4& \\ \iff \cos\widehat{A\Omega C} &= -\frac 1 4 \times \frac 4 3& \\ \iff \cos\widehat{A\Omega C} &= -\frac 1 3& \\ \implies \widehat{A\Omega C} &= \arccos\frac 1 3.& \end{aligned}\] Donc, selon la calculatrice, $\widehat{A\Omega C} \approx 109,5\text{°}$.

retour

code : 110