Corrigé du 65 P. 49

retour

1. Une perte de 25% se traduit par une multiplication par \[1 - \frac{25}{100} = 1 - 0,25 = 0,75.\] Donc au bout d'une heure, la masse de médicament restante est \[w_1 = 4 \times 0,75 = 3\:\text{mg}.\]

2. Poursuivons le calcul: \[\begin{aligned} &w_2 = 0,75w_1 = 0,75\times 3 = 2,25\;;& \\ &w_3 = 0,75w_2 = 0,75\times 2,25 = 1,6875 \approx 1,688.& \end{aligned}\] Au bout de 3 heures, il reste environ 1,688 mg de médicament dans le sang.

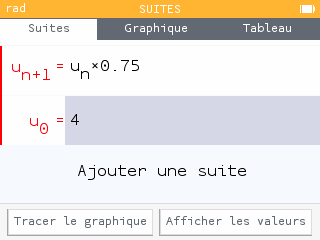
3. Chaque heure, la masse de médicament est multipliée par 0,75. La suite $(w_n)$ est donc géométrique de raison $q=0,75$.
Son premier terme est $w_0 = 4$.

4. Puisque $0 < q < 1$, la suite $(w_n)$ est décroissante.

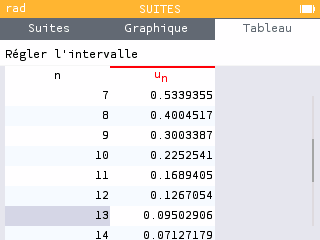
5. A l'aide de la calculatrice, on constate que \[w_{12} \approx 0,128 > 0,1 \quad\text{mais}\quad w_{13} \approx 0,095 < 0,1.\] Donc au bout de 13 heures, la quantité de médicament dans le sang sera devenue inférieure à 10^-1 mg.

retour