1. Généralités sur les vecteurs

1.1. Notion de vecteur

Déf. 1.1.1. Soient $A$ et $B$ deux points distincts du plan. Le vecteur $\overrightarrow{AB}$ désigne tout à la fois :

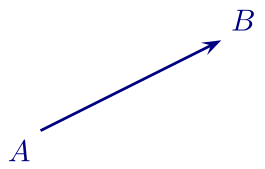
la direction du segment $[AB]$;
(des segments ont même direction quand ils sont parallèles)
le sens de parcours de $A$ vers $B$;
la longueur $AB$.

Ex. 1.1.2. Dans la figure ci-dessous,

$\vec u$ et $\vec v$ ont le même sens mais pas la même direction.
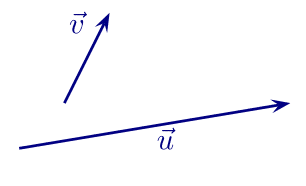
Dans la figure ci-dessous,

$\vec u$ et $\vec v$ ont la même direction mais pas le même sens.
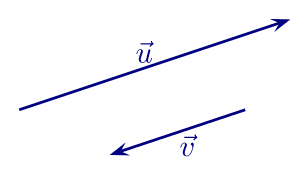
Dans la figure ci-dessous,

$\vec u$ et $\vec v$ n'ont ni la même direction, ni le même sens.

Déf. 1.1.3. $\overrightarrow{AA} = \vec 0$ est le vecteur nul.
Sa longueur est nulle, il a toutes les directions et tous les sens possibles.

Déf. 1.1.4. La longueur $AB$ s’appelle aussi la norme du vecteur $\overrightarrow{AB}$ et se note $\lVert\overrightarrow{AB}\rVert$.

1.2. Caractérisation de vecteurs égaux

Prop. Soient $A$, $B$, $C$ et $D$ quatre points.

$\overrightarrow{AB} = \overrightarrow{CD}$ ssi $ABDC$ est un parallélogramme.
$\overrightarrow{AB} = \overrightarrow{BC}$ ssi $B$ est le milieu de $[AC]$.

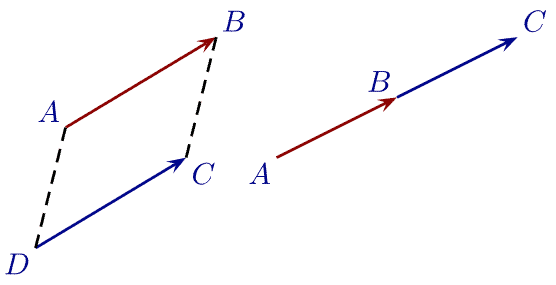
1.3. Translation

Déf. Soit $\vec u$ un vecteur. On appelle translation de vecteur $\vec u$ la transformation du plan qui, à tout point $M$, fait correspondre le point $M'$ tel que $\overrightarrow{MM'}=\vec u$.

2. Somme de vecteurs

2.1. Relation de Chasles

Déf.2.1.1. Soient $A$, $B$ et $C$ trois points. \[\overrightarrow{A{\color{Red}B}}+\overrightarrow{{\color{Red}B}C} = \overrightarrow{AC}.\]

Pour construire une somme de vecteurs, on utilise la relation de Chasles et le "principe" suivant : un vecteur peut être représenté où on le souhaite dans le plan.
On peut donc redessiner l'un des deux vecteurs pour qu'ils soit en configuration de Chasles, c.a.d. que la fin du premier soit aussi le début du second.

Ex. 2.1.2. Dans les exemples suivants, le vecteur qui a été redessiné est en pointillés verts.

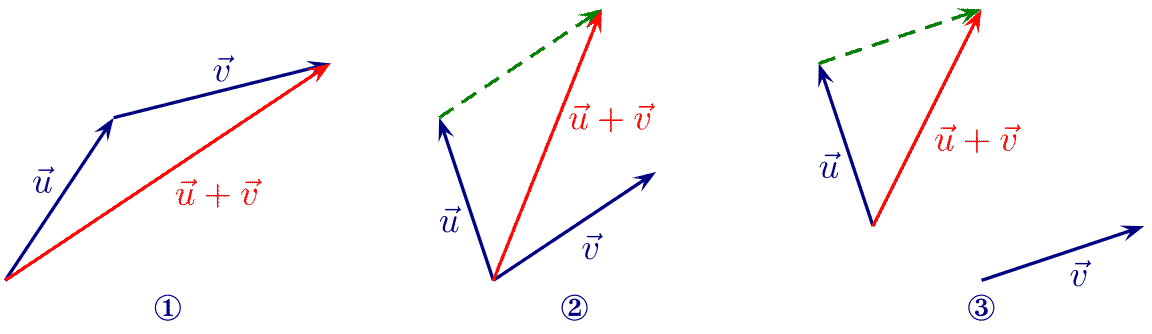
2.2. Opposé d'un vecteur

Pour tous points $A$ et $B$. \[\overrightarrow{AB}+\overrightarrow{BA}= \overrightarrow{AA} = \vec 0.\] Cela nous mène à la définition suivante.

Déf. 2.2.1 Pour tous points $A$ et $B$, $\overrightarrow{BA}$ est l'opposé du vecteur $\overrightarrow{AB}$.
On le note $\overrightarrow{BA} = -\overrightarrow{AB}$.

Rem. 2.2.2. Un vecteur et son opposé ont même direction et même longueur, mais des sens différents.

2.3. Propriétés de l'addition vectorielle

Prop. 2.2.3.(admises) L'addition vectorielle a les mêmes propriétés que l'addition des nombres.
Par exemple :

$\vec u + \vec v = \vec v + \vec u$ (commutativité);
$(\vec u + \vec v) + \vec w = \vec u + (\vec v + \vec w) = \vec u + \vec v + \vec w$ (associativité)
$\vec u + \vec 0 = \vec 0 + \vec u = \vec u$;
$-(\vec u + \vec v) = -\vec u - \vec v$.

3. Produit d'un vecteur par un réel

3.1. Valeur absolue

Déf. 3.1.1. Soit $x$ un nombre réel. On appelle valeur absolue de $x$ le nombre $\lvert x \rvert$ défini par

Si $x\ge 0$, $\lvert x \rvert = x$;
Si $x < 0$, $\lvert x \rvert = -x$.

Ex. 3.1.2. $\lvert 5 \rvert = 5$; $\lvert -2 \rvert = -(-2) = 2$.

Quand $x$ est positif, $\lvert x \rvert$ est $x$ lui-même. Quand $x$ est négatif, $\lvert x \rvert$ est l'opposé de $x$, donc encore un nombre positif.
En quelque sorte, la valeur absolue est une "machine à rendre positif".

Prop. 3.1.3.

Pour tout réel $x$, $\lvert x \rvert \ge 0$.
On a l'équivalence: \[\lvert x\rvert = 0 \iff x = 0.\]

Preuve. La preuve du premier point a été réalisée juste avant.
Si $x$ est égal à $0$, alors puisque $0$ est positif \[\lvert 0 \rvert = 0.\] Réciproquement, si $\lvert x \rvert = 0$, cela signifie soit que $x=0$, soit que $-x=0$. Dans les deux cas, $x=0$.

3.2. Produit d'un vecteur par un réel

Déf. 3.2.1. Soit $\vec u$ un vecteur et $k$ un nombre réel.
$k\vec u$ est le produit de $\vec u$ par $k$.
C'est le vecteur tel que :
- $k\vec u$ et $\vec u$ ont la même direction;
- $\lVert k\vec u\rVert = \lvert k \rvert \times \lVert \vec u \rVert$;
- Si $k\ge 0$, $\vec u$ et $k\vec u$ ont même sens. Sinon ils sont de sens contraires.
Ex. 3.2.2.

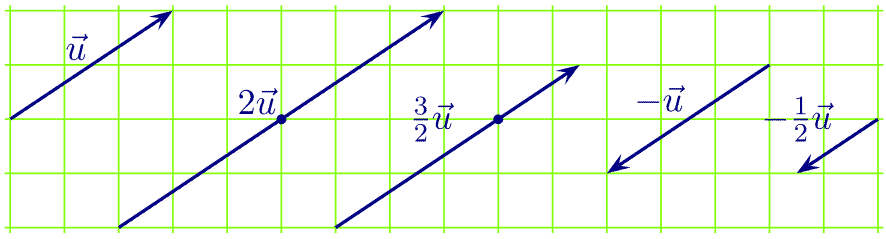
3.3. Propriétés

Les propriétés de la somme et du produit d'un vecteur par un réel sont similaires à celles de ces opérations sur les nombres.
Par exemple.

Prop. 3.3.1. (admises) Soient $a$ et $b$ deux réels, $\vec u$ et $\vec v$ deux vecteurs.
- $b\left(a\vec u\right) = \left(a\times b\right)\vec u$;
- $a\left(-\vec u\right) = -a\vec u$;
- $a\left(\vec u + \vec v\right) = a\vec u + a\vec v$ (distributivité).
- $(a+b)\vec u = a\vec u + b\vec u$.