Suites numériques
Cours

retour

1. Suites numériques quelconques

1.1. Définition

Une suite numérique est une liste ordonnée infinie de nombres réels.
Chacun de ces nombres est repéré par sa position dans la liste, un entier naturel que l'on appelle son rang ou son indice.
Les rangs sont le plus souvent comptés à partir de 0 ou de 1.
On peut aussi définir une suite numérique comme suit.

Déf. Une suite numérique $(u_n)$ est une fonction définie sur $\mathbb N$ (ou $\mathbb N^*$) et à valeurs dans $\mathbb R$.
À chaque entier $n\in\mathbb N$ (ou $n\in\mathbb N^*$), elle fait correspondre un réel noté $u_n$, qui est le terme de rang $n$ (ou terme d'indice $n$) de la suite.

Ex.

Soit $(u_n)$ la suite « carré » qui à chaque entier naturel $n$ fait correspondre son carré. Alors : \[\begin{aligned} u_0 &= 0^2=0;& \quad u_1 &= 1^2=1;& \\ u_2&=2^2=4;& \quad u_5&=5^2 = 25;& \\ u_{10}&=10^2 = 100;& \quad &\ldots& \end{aligned}\]
Soit $(v_n)$ une suite de premier terme 4 et dont chaque terme est 3 de plus que le terme précédent. Ses premiers termes seront : \[\begin{aligned} v_0 &= 4;& \quad v_1 &= 7;& \quad v_2 &= 10;& \\ v_5 &= 19;& \quad v_{10} &= 33;& \quad &\ldots& \end{aligned}\]

Nous verrons plus loin que la suite $(u_n)$ est ici donnée par son terme général, tandis que la suite $(v_n)$ est donnée par une relation de récurrence.

Déf. Le plus petit rang de la suite (en général 0 ou 1) est appelé rang initial et le terme correspondant est le terme initial.

Rem. On prendra bien garde à distinguer $(u_n)$, qui désigne l'ensemble de tous les termes de la suite numérique, de $u_n$ (sans parenthèses) qui ne représente qu'un terme particulier de cette suite, le terme de rang $n$.
Puisque les suites sont des fonctions, on utilise parfois les notations propres aux fonctions : la suite $(u_n)$ est appelée simplement $u$ et le terme de rang $n$ n'est plus noté $u_n$ mais $u(n)$.

1.2. Génération d'une suite numérique

Proposons deux grandes méthodes pour définir une suite numérique $(u_n)$:

Par une formule explicite (on dit aussi "un terme général") : Dans ce cas, on donne l'expression de la fonction $f$ telle que pour tout entier naturel $n$, $u_n=f(n)$.
L'intérêt majeur du terme général est qu'il permet de calculer immédiatement n'importe quel terme de la suite dès lors que l'on connaît son rang.
Par une relation de récurrence : Dans ce cas, on donne un terme particulier (en général le terme initial), puis l'expression de la fonction $f$ telle que \[u_{n+1} = f(u_n).\] Avec une telle définition, on ne peut calculer les termes que les uns après les autres.

Ex. Si la suite $(u_n)$ est définie par le terme général \[u_n = 2n + 4\] alors ses premiers termes sont \[\begin{aligned} u_0 &= 2\times 0 + 4 =4;& \\ u_1 &= 2\times 1 + 4 = 6;& \\ u_2 &= 2\times 2 + 4 = 8;& \\ &\ldots& \end{aligned}\]
Si la suite $(v_n)$ est définie par le terme initial $u_0 = 1$ et la relation de récurrence \[u_{n+1}=2u_n + 4\] alors ses premiers termes sont \[ u_0 = 1;\quad u_1 = 2\times 1 + 4 =6;\quad u_2 = 2\times 6 +4 = 16; \ldots\]

Exercices.
EX-01 EX-02 EX-03 EX-04 EX-05 EX-06 EX-07 EX-08 EX-09 EX-10

1.3. Monotonie d'une suite

Déf. Soit $(u_n)$ une suite définie sur $\mathbb N$. Si pour tout entier naturel $n\;$:

$u_{n+1} \geqslant u_n$, alors $(u_n)$ est dite croissante ;
$u_{n+1} \leqslant u_n$, alors $(u_n)$ est dite décroissante ;
$u_{n+1}=u_n$, alors $(u_n)$ est dite constante.

Une suite croissante, décroissante ou constante est dite monotone.

Rem. On a l'équivalence \[u_{n+1} \geqslant u_n \iff u_{n+1}-u_n \geqslant 0.\] On utilise souvent cette dernière forme, car on dispose de nombreux outils pour étudier un signe.

Proposons deux autres critères permettant d'étudier la monotonie d'une suite.

Prop. Soit $(u_n)$ est une suite à termes strictement positifs. $(u_n)$ est croissante ssi : \[\forall n\in\mathbb N,\quad \frac{u_{n+1}}{u_n} \geqslant 1.\] $(u_n)$ est décroissante ssi : \[\forall n\in\mathbb N,\quad \frac{u_{n+1}}{u_n} \leqslant 1.\]

Dém.

Puisque $u_n > 0$, on a l'équivalence : \[u_{n+1} \ge u_n \iff \frac{u_{n+1}}{u_n}\ge \frac{u_n}{u_n} \iff \frac{u_{n+1}}{u_n} \ge 1.\]

Prop. Soit $f$ une fonction définie et croissante (resp. décroissante) sur $[0;+\infty[$. Alors la suite $(u_n)$ définie pour tout entier naturel $n$ par $u_n=f(n)$ est elle aussi croissante (resp. décroissante).

Dém.

(Dans le cas $f$ croissante.)
Puisque $f$ est croissante, pour tous réels positifs $x_1$ et $x_2$: \[x_1 < x_2 \implies f(x_1) \leqslant f(x_2).\] Or, quel que soit l'entier naturel $n$, $n < n+1$. Donc : \[f(n) \leqslant f(n+1) \implies u_n \leqslant u_{n+1}.\]

Exercices
EX-11 EX-12 EX-13 EX-14 EX-15 EX-16* EX-17 EX-18 EX-19 EX-20

2. Suites particulières

2.1. Suites arithmétiques

Déf. Soit $r$ un réel. On appelle suite arithmétique de raison $r$ toute suite $(u_n)$ qui vérifie la relation \[ \forall n\in\mathbb N,\qquad u_{n+1} = u_n + r.\]

Rem. Si $(u_n)$ est arithmétique de raison $r$: \[\begin{aligned} u_{\color{Red}0} &= u_0 + 0 = u_0+{\color{Red}0} r;&\\ u_{\color{Red}1} &= u_0+r = u_0+{\color{Red}1}r;&\\ u_{\color{Red}2} &= u_1+r = u_0 + 1r + r = u_0+{\color{Red}2}r;&\\ u_{\color{Red}3} &=u_2+r = u_0 + 2r + r = u_0 +{\color{Red}3}r;&\\ &\text{etc}\ldots& \end{aligned}\] À défaut de la démontrer, cette remarque permet de conjecturer la relation suivante.

Prop. Soit $(u_n)$ une suite de premier terme $u_0$ (resp. $u_1$). $(u_n)$ est arithmétique de raison $r$ si et seulement si, \[\begin{aligned} \forall n\in\mathbb N,\ u_n &= u_0 + nr& \\ &\text{(resp.)}& \\ \forall n\in\mathbb N^*,\ u_n &= u_1+(n-1)r.& \end{aligned}\]

2.2. Suites géométriques

Déf. Soit $q\in\mathbb R$. On appelle suite géométrique de raison $q$ toute suite qui vérifie la relation \[\forall n\in\mathbb N,\qquad u_{n+1} = qu_n.\]

Rem. Si $(u_n)$ est géométrique de raison $q$: \[\begin{aligned} u_{\color{Red}0} &= 1\times u_0 = q^{\color{Red}0} \times u_0;& \\ u_{\color{Red}1} &=qu_0 = q^{\color{Red}1}u_0;& \\ u_{\color{Red}2} &=qu_1 = q\times qu_0 = q^{\color{Red}2}u_0;& \\ u_{\color{Red}3} &=qu_2 = q\times q^2u_0 = q^{\color{Red}3}u_0;& \\ &\ldots& \end{aligned}\] À défaut de la démontrer, cette remarque permet de conjecturer la relation suivante.

Prop. Soient $q$ un réel et $(u_n)$ une suite de premier terme $u_0$ (resp. $u_1$). $(u_n)$ est géométrique de raison $q$ si et seulement si \[\begin{aligned} \forall n\in\mathbb N,\ u_n &= q^n u_0& \\ &\text{(resp.)}& \\ \forall n\in\mathbb N^*,\ u_n &= u_1q^{n-1}.& \end{aligned}\]

Exercices
Déterminer la nature d'une suite.
EX-21 EX-22 EX-23 EX-24
(Avec la fonction exponentielle)
EX-25 EX-26
Terme général d'une suite arithmétique ou géométrique.
EX-27 EX-28 EX-29 EX-30 EX-31 EX-32
Divers sur suites arithmétiques ou géométriques.
EX-33 EX-34 EX-35

3. Limite

Étudier la limite d'une suite $(u_n)$, c'est se demander ce qu'elle devient lors $n$ devient "infiniement" grand.

Si les termes de la suite finissent par dépasser n'importe quel réel qu'on aura pu choisir, on dit que la suite a pour limite "plus l'infini" (ou que la suite tend vers "plus l'infini"). On le note \[\displaystyle\lim_{n\to+\infty} u_n = +\infty.\]
Si les termes de la suite finissent par être inférieurs à n'importe quel réel qu'on aura pu choisir, on dit que la suite a pour limite "moins l'infini". On le note \[\displaystyle\lim_{n\to+\infty} u_n = -\infty.\]
S'il existe un certain réel $\ell$ tel que que les termes de la suite finissent par être aussi proche qu'on l'aura décidé de $\ell$, on dit que la suite a pour limite $\ell$ (ou que la suite tend vers $\ell$). On le note \[\displaystyle\lim_{n\to+\infty} u_n = \ell.\]
Dans ce cas, et ce cas seulement, on dit aussi que la suite $(u_n)$ converge vers $\ell$.

Dans le cadre du cours de première, il ne s'agira que de conjecturer la limite éventuelle d'une suite. Ce point sera largement revu dans le cours de terminale.

4. Sommes de termes

Le résultat suivant permet de calculer des sommes de termes de suites arithmétiques.

Prop. \[\forall n\in\mathbb N,\quad \sum_{i=0}^n i = 0+1+2+\cdots+n = \frac{n(n+1)}2.\]

Dém.

(Démonstration "chinoise" à l'aide d'une figure.)

Dans la figure ci-dessus, les carrés bleutés représentent la somme $S$.
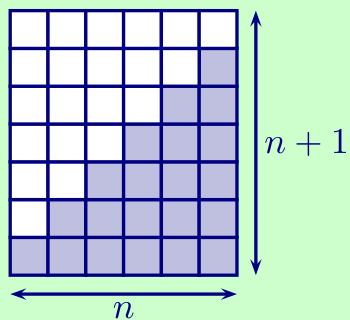
Les carrés blancs représentent aussi la somme $S$.
Regroupés, en rectangle, il y a donc $2S$ petits carrés.
Mais le nombre de petits carrés est aussi donné par les dimensions du rectangle : \[n\times (n+1).\] Donc \[S = \frac{n(n+1)}2.\]

Prop. Soit $(u_n)$ une suite arithmétique de premier terme $u_0$ et de raison $r$. Alors : \[\forall n\in\mathbb N,\quad \sum_{i=0}^n u_i = u_0 + u_1 + \cdots + u_n = (n+1)\frac{u_0 +u_n} 2.\] La somme des termes $u_0$, $u_1$ jusqu'à $u_n$ est donc égale à la moyenne des termes extrêmes $\frac{u_0+u_n}2$ multipliée par le nombre de termes $(n+1)$.

Dém.

\begin{align*} S &=\underbrace{u_0 + u_1 + u_2 + \cdots + u_n}_{n+1\ \text{termes}} \\ &= u_0 + u_0+1\times r + u_0+2\times r + \cdots + u_0 + nr \\ &=(n+1)u_0 + (1+2+\cdots+n)r& \\ &=(n+1)u_0 + \frac{n(n+1)}2r& \\ &=(n+1)\left(u_0 +\frac{n}2r\right)& \\ &=(n+1)\frac{2u_0 + nr}2& \end{align*} Enfin, puisque \[2u_0+nr = u_0 + u_0 + nr = u_0 + u_n,\] on obtient bien que: \[S =(n+1)\frac{u_0+u_n}2.\]

La propriété suivante sert à calculer des sommes de termes de suites géométriques.

Prop. Soit $q$ un réel différent de 1. Alors : \[ \forall n\in\mathbb N,\quad \sum_{i=0}^n q^i = q^0 + q^1 + q^2 + \cdots +q^n = \frac{1-q^{n+1}}{1-q}.\]

Dém.

Si l'on note \[ S= 1 + q + q^2 + \cdots + q^n\] alors on a : \[\small qS = q(1+q+q^2 + \cdots + q^n) = q^1 + q^2 + q^3 + \cdots + q^{n+1}.\] Donc: \[\begin{aligned} S - qS &= q^0 - q^{n+1}& \\ \iff (1-q)S &= 1-q^{n+1}& \\ \iff S &= \frac{1 - q^{n+1}}{1-q}.& \end{aligned}\]

Prop. Soit $(u_n)$ une suite géométrique de premier terme $u_0$ et de raison $q\neq 1$. Alors \[\forall n\in\mathbb N,\quad \sum_{i=0}^n u_i = u_0\frac{1-q^{n+1}}{1-q}.\]

Dém.

\begin{align*} S &=u_0 + u_1 + u_2 + \cdots + u_n& \\ &=u_0 + u_0q + u_0q^2 + \cdots + u_0q^n& \\ &=u_0\left(1 + q + q^2 + \cdots + q^n\right)& \\ &=u_0\frac{1-q^{n+1}}{1-q}.& \end{align*}

Exercices
EX-36 EX-37 EX-38 EX-39