0. Rappels

On pourra éventuellement consulter le cours de seconde sur les probabilités.

Voir probabilités seconde

1. Notion de probabilité conditionnelle

Soient, dans une expérience aléatoire donnée, deux événements $A$ et $B$, $A$ étant de probabilité non nulle.

Supposons que $A$ soit réalisé. Quelle est alors la probabilité d'obtenir $B$ ? Cette probabilité s'appelle probabilité de $B$ sachant $A$ réalisé et se note $P_A(B)$.

Ex. On tire une carte au hasard dans un jeu de 32 cartes. On note $F$ l'événement « la carte tirée est une figure (roi, dame ou valet) » et $R$ l'événement « la carte tirée est un roi ».

La personne qui tire la carte annonce qu'il s'agit d'une figure. Quelle est la probabilité $P_F(R)$ que ce soit un roi ?

On sait que la carte tirée est l'une des 12 figures du jeu, et qu'il y a quatre rois parmi les figures. Donc : \[P_F(R) = \frac 4 {12} = \frac 1 3.\]

Déf. Soit $A$ un événement de probabilité non nulle. Alors, pour tout événement $B$, on appelle probabilité de $B$ sachant $A$: \[P_A (B)=\frac{P(A\cap B)}{P(A)}\]

Prop. D'après la relation précédente: \[P(A\cap B)=P(A)\times P_A(B).\]

Prop. Soit $A$ un événement de probabilité non nulle. La probabilité $P_A$ a toutes les propriétés d'une probabilité ordinaire. En particulier, pour tout événement $B$: \[P_A(\overline B) = 1 - P_A(B).\]

Exercices corrigés
EX-01 EX-02 EX-03 EX-04 EX-05 EX-06 EX-07

2. Arbre de probabilités, loi des probabilités totales

Déf. Une famille d’événements $\{A,B,C\}$ forme une partition de l’univers (ou un système complet d’événements) ssi : \begin{gather} A\neq \emptyset,\quad B\neq \emptyset,\quad C\neq \emptyset.\\ A\cap B = A\cap C = B\cap C =\emptyset.\\ A \cup B \cup C = \Omega. \end{gather}

Rem. En particulier, quel que soit l'événement $A$ non vide, $\{A,\overline A\}$ est une partition de l'univers.

Soit une partition de l'univers (ici $\{A;B;C\}$) et un événement $D$.
On peut modéliser la situation à l’aide d’un arbre appelé arbre de probabilités ou arbre pondéré.

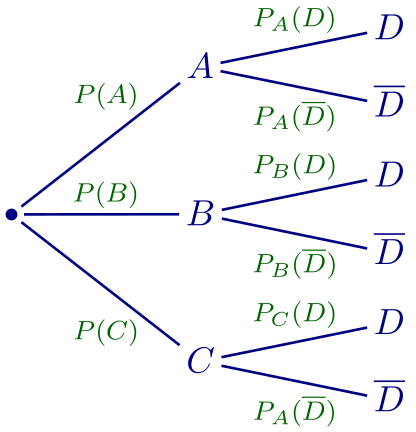
On peut remarquer que :

On a $P(A)+P(B)+P(C) = 1$ et $P_A(D)+P_A(\overline D) = 1$.
Plus généralement, la somme des pondérations des branches partant d'un même sommet est toujours égale à 1.
$p(A\cap B) = P(A) \times P_A(D)$.
Plus généralement, la probabilité d'une intersection d'événements s'obtient en multipliant les pondérations des branches menant aux événements de cette intersection.

Prop. (loi des probabilités totales.) Si $\{A,B,C\}$ est une partition de l’univers, alors pour tout événement $D$: \[\begin{aligned} P(D)&=P(A\cap D) + P(B\cap D) + P(C\cap D)& \\ &=P(A)\times P_A(D) + P(B)\times P_B(D) + P(C) \times P_C(D).& \end{aligned}\]

Coro. Si $A$ et $B$ sont deux événements avec $P(B)\in ]0;1[$: \[\begin{aligned} P(A) &= P(A\cap B) + P(A\cap\overline B)& \\ &=P_B(A)\times P(B) + P_{\overline B}(A)\times P(\overline B).& \end{aligned}\]

Exercices corrigés

EX-08 EX-09 EX-10 EX-11 EX-12 EX-13 EX-14
EX-15 EX-16 EX-17

3. Indépendance

Prop. & déf. Deux événements $A$ et $B$ de probabilités non nulles sont indépendants si le fait que l'un d'eux soit réalisé ne modifie pas la probabilité de voir l'autre se réaliser.
Autrement dit, $A$ et $B$ sont indépendants si et seulement si \[\begin{aligned} P_B(A) &= P(A)& \\ \iff P(A\cap B) &= P(A)\times P(B)& \\ \iff P_A(B) &= P(B).& \end{aligned}\]

Exercices corrigés

EX-18 EX-10 EX-20 EX-21 EX-22 EX-23 EX-24

4. Expériences aléatoires successives

Il s'agit d'étudier la répétition d'expériences aléatoires successives à l'aide d'un arbre de probabilité. Pas de cours à retenir pour cette section.

Exercices corrigés

EX-25 EX-26 EX-27 EX-28 EX-29*