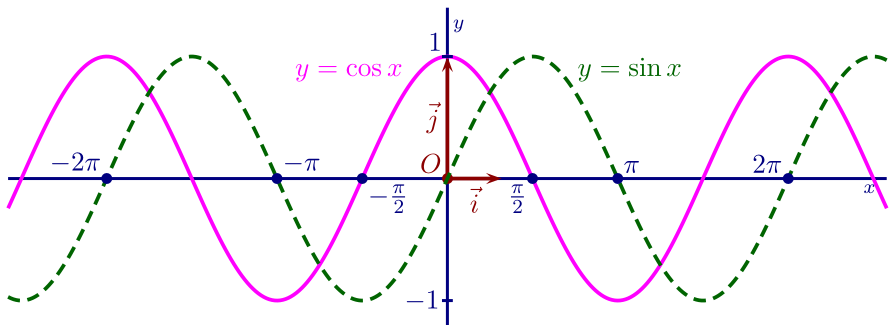
Fonctions trigonométriques
Cours
retour
0. Rappels : trigonométrie dans le triangle rectangle
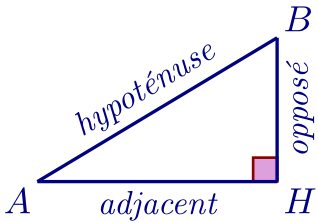
def. Soit $AHB$ un triangle rectangle en $H$, donc d'hypoténuse $[AB]$. Si l'on s'intéresse à l'angle $\hat A$, alors $[AH]$ est le côté adjacent à $\hat A$ tandis que $[HB]$ est le côté opposé à $\hat A$.
Prop. & def.
Pour une mesure de $\hat A$ donnée, les rapports de longueurs $\dfrac{AH}{AB}$,
$\dfrac{BH}{AB}$ et $\dfrac{BH}{AH}$ sont constants.
On les appelle respectivement cosinus, sinus et tangente de l'angle $\hat A$.
\[\begin{aligned}
\cos \hat A &=\frac{\text{adjacent}}{\text{hypoténuse}}= \frac{AH}{AB},&
\\
\sin\hat A &=\frac{\text{opposé}}{\text{hypoténuse}}= \frac{BH}{AB},&
\\
\tan \hat A &=\frac{\text{opposé}}{\text{adjacent}} = \frac{BH}{AH}.&
\end{aligned}\]
Rem. Ici l'angle $\hat A$ a une mesure comprise entre 0° et 90°.
Exercices
Ex. 01
Ex. 02
Ex. 03
Ex. 04*
Ex. 05
Ex. 06
Ex. 07*
Ex. 08*
Ex. 09
Ex. 10
Ex. 11
1. Angles en radians
1.1. Angle au centre et arc intercepté
Prop. Soit un cercle de centre $O$, $A$ et $B$ deux points du cercle. La longueur de l'arc $\overset{\frown}{AB}$ intercepté par l'angle $\widehat{AOB}$ est proportionnelle à l'angle au centre $\widehat{AOB}$.
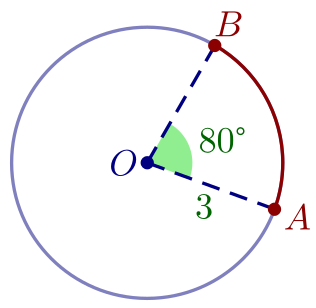
Ex.
Soit dans la figure ci-contre deux points $A$ et $B$ situés sur un cercle de centre $O$ et de
rayon 3 et tels que $\widehat{AOB}=80°$.
Calculer la longueur de l'arc $\overset{\frown}{AB}$.
Le périmètre du cercle mesure
\[2\pi R = 2\pi \times 3 = 6\pi.\]
Puisque la longueur de l'arc est proportionnelle à l'angle au centre:
\[\overset{\frown}{AB} = \frac{80}{360}\times 6\pi = \frac 4 3\pi.\]
1.2. Définition
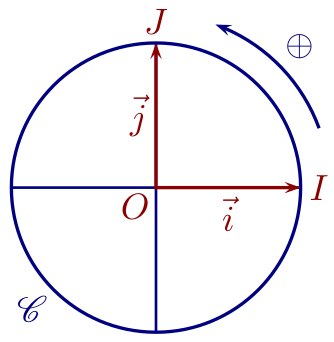
Def.
Le cercle trigonométrique $\mathscr C$ est un cercle de centre $O$ et de rayon 1.
On a défini sur ce cercle un sens de parcours direct (en général « tourner dans le sens
inverse des aiguilles d'une montre »), l'autre sens de parcours étant qualifié d'indirect.
Il est de plus muni d'un repère orthonormé $(O;\overrightarrow{OI},\overrightarrow{OJ})$ direct,
ce qui signifie que l'on peut se déplacer de $I$ à $J$ en réalisant un quart de tour dans le
sens direct.
Def. Pour tout point $M$ de $\mathscr C$, on appelle mesure en radians de l'angle de vecteurs $\left(\overrightarrow{OI},\overrightarrow{OM}\right)$ un réel $x$ tel que :
- $\lvert x \rvert$ est la distance que parcourt un point mobile $M$ en se déplaçant de $I$ vers $M$.
- Si ce déplacement se fait dans le sens direct, $x$ est positive. Sinon, $x$ est négative.
Ex. Quelques mesures d'angles.
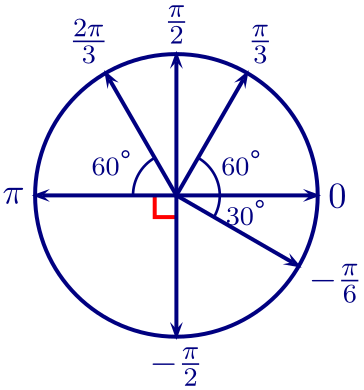
Rem. On peut prendre pour $x$ la longueur de n'importe quel déplacement qui va de $A$ à $M$. Il y a donc une infinité de mesures possibles pour un angle donné.
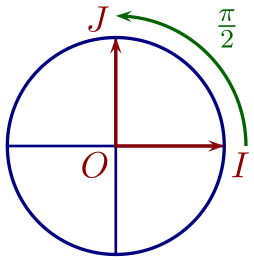
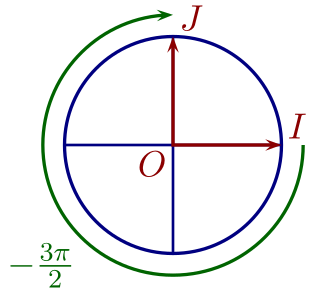
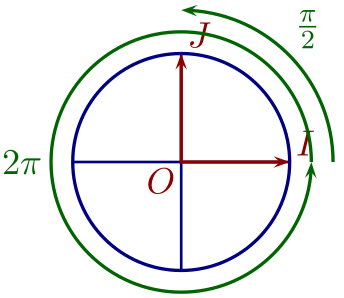
Finalement, pour créer différentes mesures d'un angle, il suffit de prendre l'une d'entre-elle $x$ et d'ajouter ou d'enlever un nombre entier $k$ de tours, chaque tour mesurant $2\pi$.
On obtient donc la propriété suivante.
Prop. Si $x$ est une mesure d'un angle de vecteurs $(\vec u,\vec v)$, alors toutes les mesures de cet angle sont de la forme \[x + 2k\pi\] où $k$ est n'importe quel entier relatif.
Ex. Si $(\vec u,\vec v) = \dfrac \pi 3$, alors on a aussi, par exemple : \[\begin{aligned} (\vec u,\vec v)&= \frac \pi 3 + 2\pi = \frac{7\pi} 3\;;& \\ (\vec u,\vec v) &= \frac \pi 3 - 2\pi = -\frac{5\pi} 3\;;& \\ (\vec u, \vec v) &= \frac \pi 3 + 5\times 2\pi = \frac{31\pi}3\;;& \\ (\vec u,\vec v) &=\frac \pi 3 - 3\times 2\pi = -\frac{17\pi}3.& \end{aligned}\]
Def. La mesure principale d'un angle de vecteurs est celle dont la valeur absolue est la plus petite. C'est l'unique mesure située dans l'intervalle $]-\pi\;;\;\pi]$.
Exercices
Ex. 12
Ex. 13
Ex. 14
Ex. 15
Ex. 16
2. Trigonométrie
2.1. Définitions
Def.
Soit $\mathscr C$ un cercle trigonométrique muni de son repère orthonormé direct
$(O;\overrightarrow{OI},\overrightarrow{OJ})$.
À tout réel $x$, on peut faire correspondre l'unique point $M$ de $\mathscr C$ tel que
\[(\overrightarrow{OI},\overrightarrow{OM}) = x.\]
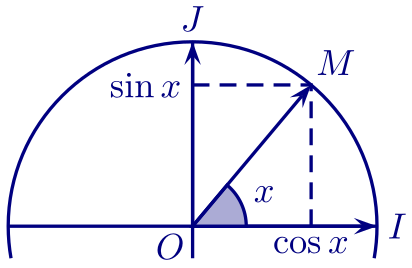
- On appelle cosinus de $x$, noté $\cos x$ ou $\cos(x)$, l'abscisse de $M$.
- On appelle sinus de $x$, noté $\sin x$ ou $\sin(x)$, l'ordonnée de $M$.
Rem. Une calculatrice scientifique sait calculer une valeur arrondie du cosinus ou du sinus d'un réel,
- à condition d'être en mode radian
Elle est également capable de donner une valeur arrondie d'un réel $x$ de cosinus ou de sinus donné (fonctions appelées acos et asin, parfois cos-1 et sin-1).
2.2.Propriétés
Prop. Pour tout réel $x$, $-1\le \cos x\le 1$ et $-1\le \sin x \le 1$.
Prop. (Relation fondamentale de la trigonométrie.) Pour tout réel $x$, \[\cos^2 x + \sin^2 x = 1.\]
Prop. (Angles associés.) Pour tout réel $x$: \[\begin{aligned} \cos(-x) &=\cos x\;;&\qquad \sin(-x) &=-\sin x.& \\ \cos(\pi - x) &= -\cos x\;;&\qquad \sin(\pi-x) &= -\sin x.& \\ \cos\left(\frac \pi 2 - x\right) &=\sin x\;;& \sin\left(\frac \pi 2 - x\right)&=\cos x.& \end{aligned}\]
Prop. (Valeurs particulières.) \[\begin{array}{|l|c|c|c|c|c|c|} \hline \rule[-.8em]{0em}{2.2em}x & 0 & \frac \pi 6 & \frac \pi 4 & \frac \pi 3 & \frac \pi 2 & \pi \\ \hline \rule[-.8em]{0em}{2.2em}\cos x & 1 & \frac{\sqrt 3} 2 & \frac 1 {\sqrt 2} = \frac{\sqrt 2} 2 & \frac 1 2 & 0 & -1 \\ \hline \rule[-.8em]{0em}{2.2em}\sin x & 0 & \frac 1 2 & \frac 1 {\sqrt 2} = \frac{\sqrt 2} 2 & \frac{\sqrt 3} 2 & 1 & 0 \\ \hline \end{array}\]
Exercices
Équations trigonométriques.
Ex. 17
Ex. 18
Ex. 19
Ex. 20*
Ex. 21
Ex. 22
3. Fonctions trigonométriques
3.1. Parité
Prop. & def.
On a vu que pour tout réel $x$,
\[\cos(-x) = \cos x.\]
On le traduit en disant que la fonction cosinus est paire.
Cela entraîne que sa courbe est symétrique par rapport à l'axe des ordonnées.
Prop. & def.
Pour tout réel $x$,
\[\sin(-x) = -\sin x.\]
On le traduit en disant que la fonction sinus est impaire.
Cela entraîne que sa courbe est symétrique par rapport à l'origine du repère.
3.2. Périodicité
Def. Soit $P>0$ et $f$ une fonction définie sur $\mathbb R$. $f$ est dite périodique de période $P$ si, pour tout réel $x$, \[f(x+P) = f(x).\]
Prop.
Soit $\mathscr C$ la courbe représentative d'une fonction $f$ périodique de période $P$
dans un repère $(O;\vec i,\vec j)$.
$\mathscr C$ est invariante par une translation de vecteur $P\vec i$.
Prop.
Pour tout réel $x$,
\[\cos(x + 2\pi)=\cos x\ \text{et}\ \sin(x+2\pi)=\sin x.\]
Donc sinus et cosinus sont des fonction périodiques de période $2\pi$.
Les courbes des fonctions sinus et cosinus sont donc invariantes par une translation de
vecteur $2\pi\vec i$.
3.3. Courbes représentatives