exercice SUP-08/01
retour
Partie A
1 En ajoutant 15 g de chlore, on augmente le taux de chlore de: \[\frac{15}{50\times 10000} = 0,0003\:\text{g.L}^{-1} = 0,3\:\text{mg.L}^{-1}.\]
2.a.
Soit $\mathscr A(n)$ l'assertion «$v_n \le v_{n+1} \le 4$».
(Initialisation.) On a $v_1 = 0,92\times 0,7 + 0,3 = 0,944$.
Donc $v_0 \le v_1 \le 4$; $\mathscr A(0)$ est vérifiée.
(Hérédité). Si, pour $n$ quelconque fixé, $\mathscr A(n)$ est vraie, alors:
\[\begin{aligned}
&v_n \le v_{n+1} \le 4&
\\ \implies
&0,92v_n \le 0,92v_{n+1} \le 0,92\times 4&
\\ \implies
&0,92v_n + 0,3 \le 0,92v_{n+1} + 0,3 \le 0,92\times 4 + 0,3&
\\ \implies
&v_{n+1} \le v_{n+2} \le 3,98&
\\ \implies
&v_{n+1} \le v_{n+2} \le 4.&
\end{aligned}\]
Donc $\mathscr A(n+1)$ est aussi vraie.
Donc, par récurrence, pour tout entier naturel $n$, $\mathscr A(n)$ est vraie.
2.b.
On a montré dans la question précédente que $(v_n)$ est croissante mais majorée par 4.
Elle est donc convergente.
Puisque $v_{n+1} = f(v_n)$ avec $f$ définie sur $[0;4]$ par $f(x) = 0,92x + 0,3$ et que $f$ est
continue sur $[0,4]$, alors la limite $\ell$ de $(v_n)$ vérifie la relation:
\[\begin{aligned}
\ell &= f(\ell)&
\\ \iff
\ell &= 0,92\ell + 0,3&
\\ \iff
\ell - 0,92\ell &= 0,3&
\\ \iff
0,08\ell &= 0,3&
\\ \iff
\ell &= \frac{0,3}{0,08} = 3,75.&
\end{aligned}\]
La suite $(v_n)$ converge vers 3,75.
3. Puisque $\displaystyle\lim_{n\to+\infty} v_n = 3,75$, à long terme le taux de chlore dans la piscine sera voisin de 3,75 mg.L-1, donc supérieur au taux maximum recommandé par les experts.
4.
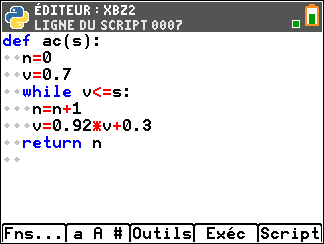
Le code complété est donné ci-dessous.
Puisque le calcul s'arrête quand $v > s$, la boucle "while" doit
se poursuivre tant que $v \le s$.
À chaque passage dans la boucle, on calcule le terme suivant de la suite $(v_n)$, donc $n$ augmente de 1.
On utilise ensuite la relation de récurrence définissant $(v_n)$ pour actualiser la valeur de v.
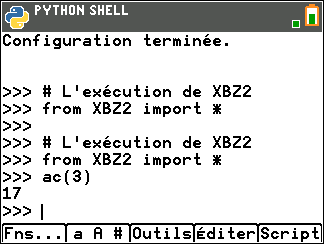
5. Réponse: 17.
-
On peut saisir le programme sur un calculatrice programmable en Python (ci-dessous, sur une TI-83)
-
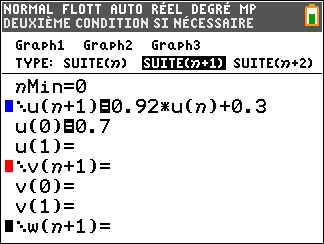
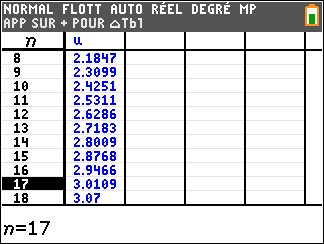
On peut programmer le calcul des termes de la suite $(v_n)$ et chercher le premier d'entre-eux qui dépasse 3
(ci dessous sur une TI-83).
Partie B
1.
D'après le cours, les solutions sur $\mathbb R$ de l'équation différentielle:
\[y' = ay + b\qquad(a\neq 0)\]
sont les fonctions définies sur $\mathbb R$ par
\[x\mapsto C\mathrm e^{ax} - \dfrac b a\]
où $C$ est une constante réelle quelconque.
Ici $a=-0,08$ et $b = \dfrac q{50}$, donc $f$ est de la forme:
\[\begin{aligned}
f(x) &= C\mathrm e^{-0,08x} - \frac{\frac q{50}}{-0,08}&
\\
&= C\mathrm e^{-0,08x} + \frac q{0,08\times 50}&
\\
&=C\mathrm e^{-0,08x} + \frac q 4.&
\end{aligned}\]
2.a. Quelle que soit la valeur du réel $C$: \[\begin{aligned} &\displaystyle\lim-{x\to+\infty} -0,08x = -\infty& \\ \implies &\lim_{x\to+\infty}\mathrm e^{-0,08x} = 0& \\ \implies &\lim_{x\to+\infty} C\mathrm e^{-0,08x} = 0.& \end{aligned}\] Donc: \[\lim_{x\to+\infty} f(x) = \frac q 4.\]
2.b. On veut que le taux de chlore se stabilise à 2 mg.L-1, donc que: \[\lim_{x\to+\infty} f(x) = 2 \implies \frac q 4 = 2 \implies q = 8.\] On sait d'autre part que $f(0) = 0,7$. Donc: \[\begin{aligned} f(0) &= 0,7& \\ \iff C\mathrm e^{-0,08\times 0} + 4 &= 0,7& \\ \iff C\times 1 + 4 &= 0,7& \\ \iff C &= 0,7 - 4 = -3,7.& \end{aligned}\]
retour
code : 211