corrigé AP-06/06
retour
1.a. \[\begin{aligned} f(x) &= x& \\ \iff 2x\mathrm e^{-x}&=x& \\ \iff 2x\mathrm e^{-x} - x &= 0& \\ \iff x(2\mathrm e^{-x} - 1)&=0.& \end{aligned}\] On reconnaît là un produit nul, donc:
- soit $x = 0$;
- soit \[\begin{aligned} &2\mathrm e^{-x} - 1 = 0& \\ \iff &\mathrm e^{-x} = \frac 1 2& \\ \iff &-x = \ln\left(\frac 1 2\right)& \\ \iff &x = -\ln\left(\frac 1 2\right) = \ln(2).& \end{aligned}\]
1.b.
$f= uv$ avec $u(x) = 2x$ donc $u'(x) = 2$ et $v(x) = \mathrm e^{-x}$ donc $v'(x) = -\mathrm e^{-x}$.
Donc pour tout $x\in[0;1]$:
\[f'(x) = 2\mathrm e^{-x} + 2x(-\mathrm e^{-x}) = 2(1 - x)\mathrm e^{-x}.\]
1.c.
Les facteurs $2$ et $\mathrm e^{-x}$ sont strictement positifs. De plus
\[x < 1 \implies -x > -1 \implies 1 - x > 1-1 \implies 1 - x > 0.\]
$f'$ est donc strictement positive sur $[0;1[$, ce qui entraîne que $f$ est strictement croissante sur $[0;1]$.
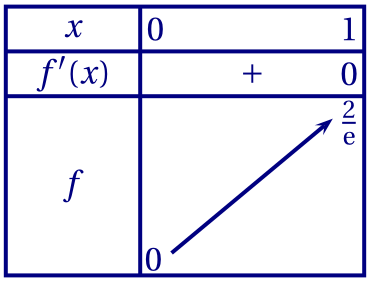
2.a.
Soit $\mathscr A(n)$ l'assertion «$0 \le u_n < u_{n+1} \le 1$».
$u_0 = 0,1$ et $u_1 = 2\times 0,1 \mathrm e^{-0,1} \approx 0,181$. Donc $\mathscr P(0)$ est vraie.
Supposons, pour $n$ quelconque fixé, que $\mathscr P(n)$ soit vraie. Alors
\[0 \le u_n < u_{n+1} \le 1.\]
$f$ étant strictement croissante sur $[0;1]$, cela entraîne que:
\[\begin{aligned}
&f(0) \le f(u_n) < f(u_{n+1}) \le f(1)&
\\ \implies
&0 \le u_{n+1} < u_{n+2} \le \ln(2).&
\end{aligned}\]
Cependant
\[2 < \mathrm e \implies \ln(2) < \ln(\mathrm e) \implies \ln(2) < 1.\]
Donc on a bien
\[0 \le u_{n+1} < u_{n+2} \le 1.\]
On a donc, pour tout entier naturel $n$: $\mathscr P(n) \implies \mathscr P(n+1)$.
Initialisée et héréditaire, $\mathscr P(n)$ est donc vraie pour tout entier naturel $n$.
2.b.
Nous venons de montrer à la fois que $(u_n)$ est (strictement) croissante et qu'elle est majorée par $1$.
Elle est donc nécessairement convergente vers un nombre réel de $[0;1]$.
3.
La fonction $f$ étant continue sur $[0;1]$, la limite $\ell$ de la suite $(u_n)$ vérifie la relation
$f(\ell) = \ell$.
Elle est donc une solution de l'équation donnée en 1.a..
$\ell$ ne saurait être égale à $0$, car $(u_n)$ est croissante et son premier terme est $u_0 = 0,1$, donc $\ell \ge 0,1$.
Donc $\ell = \ln(2)$.
4.a. La suite $(u_n)$ étant strictement croissante, chacun de ses termes est inférieur à sa limite. Pour tout entier naturel $n$: \[u_n < \ell \iff u_n < \ln(2) \iff 0 < \ln(2) - u_n.\]
4.b.
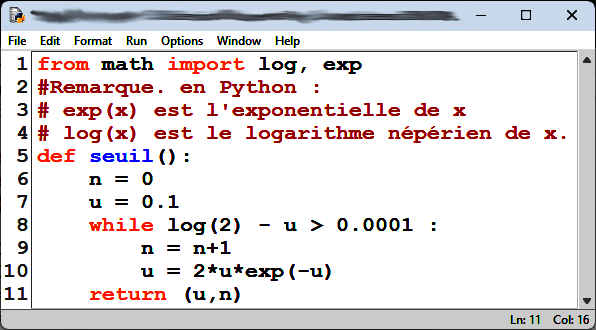
4.c.
La réponse attendue est $n=11$ (avec $u_{11} \approx 4,6272972$).
Pour répondre à la question, on peut soit implémenter le script sur une calculatrice avec Python,
soit l'exécuter à la main (à l'aide de la calculatrice).
Une méthode pour calculatrice Numworks est proposée ci-dessous en images.


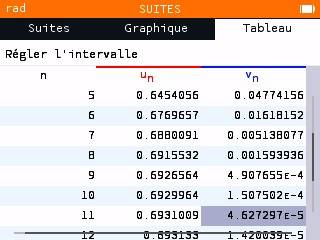
retour
code : 210