corrigé AP-06/05

retour

Partie A.

1. La fonction $f$ s'écrit $\frac u v$ où $u$ et $v$ vérifient \[u(x) = 0,96x \quad\text{et}\quad v(x) = 0,93x + 0,03.\] Ces fonctions sont dérivables sur $[0;1]$ avec \[u'(x) = 0,96 \quad\text{et}\quad v'(x) = 0,93.\] De plus, $v$ ne s'annule pas sur $[0;1]$. Donc la fonction $f$ est dérivable sur $[0;1]$ et pour tout réel $x$ de cet intervalle \begin{align*} f'(x) &= \frac{u'(x)\cdot v(x) - u(x)\cdot v'(x)}{(v(x))^2}& \\ &=\frac{0,96(0,93x + 0,03) - 0,96x\cdot0,93}{(0,93x+0,03)^2}& \\ &=\frac{0,8928x + 0,0288 - 0,8928x}{(0,93x + 0,03)^2}& \\ &=\frac{0,0288}{(0,93x+0,03)^2}.& \end{align*}

2. On sait que $0,93x+0,03$ ne s'annule pas sur $[0,1]$, donc son carré est strictement positif sur cet intervalle.
Le numérateur $0,0288$ est lui aussi strictement positif.
$f'$, quotient de deux quantités strictement positive sur $[0;1]$, est donc aussi strictement positive sur cet intervalle.
On en déduit que la fonction $f$ est strictement croissant sur $[0;1]$.

Partie B.

1. Arbre complété:

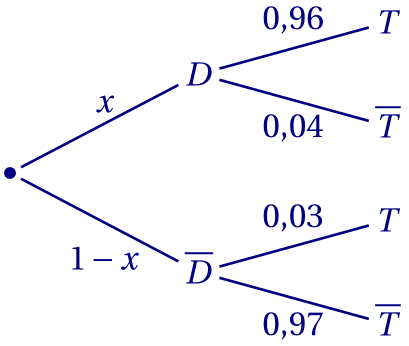
2. $P(D\cap T) = P(D)\times P_D(T) = 0,96x$.

3. $T$ et $\overline T$ formant une partition de l'univers de l'expérience: \begin{align*} P(T) &= P(D\cap T) + P(D\cap\overline T)& \\ &=0,96x + P(D)\times P_D(\overline T)& \\ &=0,96x + 0,03(1-x)& \\ &=0,96x + 0,03 - 0,03x& \\ &=0,93x + 0,03.& \end{align*}

4. On cherche: \[P_T(D) = \frac{P(D\cap T)}{P(T)} = \frac{0,96x}{0,93x + 0,03} = f(x).\] Ici, on sait que \[x = \frac{50}{1000} = 0,05.\] Donc \[P_T(D) = f(0,05) \approx 0,63.\]

5.a. On souhaite ici obtenir que: \[\begin{aligned} &P_T(D) \geqslant 0,9& \\ \iff &f(x) \geqslant 0,9& \\ \iff &\frac{0,96x}{0,93x+0,03} \geqslant 0,9& \end{aligned}\] Sachant que $0,93x + 0,03 > 0$: \[\begin{aligned} &\frac{0,96x}{0,93x+0,03} \geqslant 0,9& \\ \iff &0,96x \geqslant 0,9(0,93x + 0,03)& \\ \iff &0,96x \geqslant 0,837x + 0,027& \\ \iff &0,96x - 0,837x \geqslant 0,027& \\ \iff &0,123x \geqslant 0,027& \\ \iff &x \geqslant \frac{0,027}{0,123}.& \end{aligned}\] Puisque $\dfrac{0,027}{0,123} \approx 0,2195$, la valeur de $x$ arrondie au centième qui convient est $0,22$.

5.b. $f$ est croissante sur $[0;1]$, donc plus $x$ est grand, plus $f(x)$ est grand. En ciblant les contrôles, on augmente la proportion $x$ de sportifs dopés, donc aussi la valeur de $f(x)$.
On augmente donc la valeur prédictive positive du test.

retour

code : 209