corrigé AP-06/03

retour

Partie A

1. $p(I) = \dfrac{5,7}{100} = 0,057$.

2.a. Les tirages étant censés être indépendants (tirage avec remise), l'expérience aléatoire peut être assimilée à la répétition $n = 100$ fois d'un tirage de Bernoulli dont la probabilité de réussite est $p=0,057$.
Donc la variable $X$ qui compte le nombre de "succès" suit la loi binomiale de paramètres $n=100$ et $p=0,057$.

2.b. L'espérance de $X$ est $\operatorname E(X) = np = 100\times 0,057 = 5,7$.
Un échantillon de 100 personne donnera, en moyenne, 5,7 personnes déjà infectées.

2.c. On cherche : \[\begin{aligned} P(X = 0) &= \binom{100}{0} \times 0,057^{0} \times (1-0,057)^{100}& \\ &= 1\times 1 \times 0,943^{100} \approx 0,0028.& \end{aligned}\]

2.d. On cherche ici: $P(X \ge 2) \approx 0,9801$ (obtenu à l'aide de la calculatrice).
Sur certains modèles de calculatrice, le résultat devra être obtenu en calculant $1- P(X\le 1)$.

2.e. En réalisant des essais à la calculatrice, on obtient que $P(X\le 8) \approx 0,883$ mais que $P(X\le 9) \approx 0,941$. Donc $m = 9$.
Il y a plus de 90 % de chances qu'il y ait moins de 9 personnes déjà infectées dans un échantillon de 100 personnes.

Partie B.

1. D'après l'introduction de l'exercice, $P(I) = 0,057$.
Les informations données par le fabricant se traduisent par $P_I(T) = 0,8$ et $P_{\overline I}(\overline T) = 0,99$.
On en déduit l'arbre de probabilités suivant:

2. \[\begin{aligned} P(T) &= P(T\cap I) + P(T\cap \overline I)& \\ &=P(I)\times P_I(T) + P(\overline I)\times P_{\overline I}(T)& \\ &=0,057\times 0,8 + 0,943\times 0,01& \\ &=0,0456 + 0,00943& \\ &=0,05503.& \end{aligned}\]

3. On cherche $P_T(I)$. Par définition: \[P_T(I) = \frac{P(T\cap I)}{P(T)} = \frac{0,0456}{0,05503} \approx 0,8286.\]

Partie C

En reprenant les notations de la partie B et en notant $P(I) = p$, on peut modéliser la situation par l'arbre de probabilités suivant.

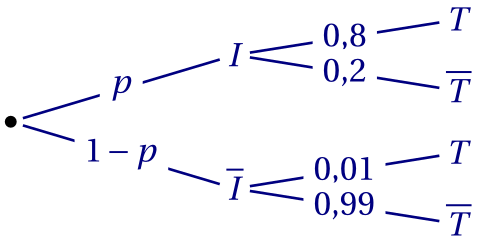
Donc: \[\begin{aligned} P(T) &= P(I\cap T) + P(\overline I \cap T)& \\ &= 0,8p + 0,01(1-p)& \\ &= 0,8p + 0,01 - 0,01p& \\ &= 0,79p + 0,01& \end{aligned}\] et d'après la consigne: \begin{align*} &P(T) = 0,2944& \\ \iff &0,79p+0,01 = 0,2944& \\ \iff &0,79p = 0,2944 - 0,01& \\ \iff &p = \frac{0,2844}{0,79} = 0,36.& \end{align*} Dans ce groupe, la probabilité d'avoir été infecté est de 36%.

retour

code : 207