corrigé AP-06/02

retour

1.a. $f=uv$ où $u$ et $v$ sont les fonctions dérivables sur $[0;10]$ telles que $u(t) = 3t$ donc $u'(t)=3$ et $v(t) = \mathrm e^{-0,5t+1}$ donc $v'(t)= -0,5\mathrm e^{-0,5t+1}$.
$f$ est donc dérivable sur $[0;10]$ avec $f'=u'v+uv'$, ce qui signifie que pour tout $t\in[0;10]$: \[f'(t) = 3\mathrm e^{-0,5t+1} + 3t\left(-0,5\mathrm e^{-0,5t+1}\right) =3\left(1 - 0,5t\right)\mathrm e^{-0,5t+1}.\]

1.b. L'exponentielle $\mathrm e^{-0,5t + 1}$ étant strictement positive, $f'(t)$ est du signe de $-0,5t + 1$.
Or : \begin{gather*} -0,5t + 1 = 0 \iff -0,5t = -1 \iff t = \frac{-1}{-0,5} = 2 \\ -0,5t + 1 > 0 \iff -0,5t > -1 \iff t < 2. \end{gather*} On en déduit le tableau de variation suivant

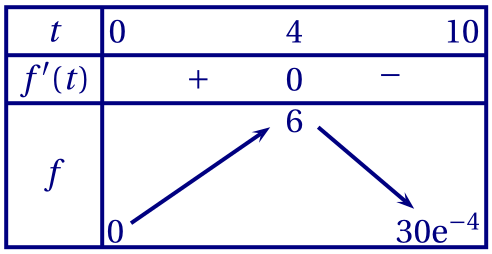
1.c. Selon le tableau de variations, $f$ admet pour maximum 6 atteint en 2. La quantité maximale de médicament dans le sang sera atteinte au bout de deux heures et sera alors de 6 mg.

2.a. Sur l'intervalle $[0;2]$, la fonction $f$ est continue et passe de $f(0) = 0$ à $f(2) = 6$. De plus, elle est strictement croissante.
Donc tout réel de l'intervalle $[0;6]$ admet un unique antécédent dans $[0;2]$ par la fonction $f$.
C'est donc en particulier le cas de 5. L'équation $f(t) = 5$ admet donc une unique solution $\alpha$ sur $[0;2]$.
À l'aide de la calculatrice, on obtient que $f(1,022)\approx 4,9996$ et $f(1,023)\approx 5,002$. Donc $\alpha \approx 1,02$.

2.b. Le médicament est efficace sur la durée: \[\beta - \alpha \approx 3,46 - 1,02 \approx 2,44\ \text{h}.\] Soit 2 heures et 0,44×60≈26 minutes.

Partie B

1. Au bout d'une heure, il reste 70 % du médicament dans le sang. On ajoute alors 1,8 mg. Donc: \[u_1 = \frac{70}{100} \times 2 + 1,8 = 1,4 + 1,8 = 3,2\ \text{mg.}\]

2. Au bout de $n$ heures, il reste $u_n$ mg de médicament. Une heure après, le patient à conservé 70% du médicament et s'en voit alors injecter 1,8 mg de plus. Donc la quantité au bout de $n+1$ heures est: \[u_{n+1} = \frac{70}{100} u_n + 1,8 = 0,7u_n + 1,8.\]

3.a. Appelons $\mathscr A(n)$ l'assertion «$u_n \leq u_{n+1} < 6$.
On sait que $u_0 = 2$ et $u_1 = 3,2$, donc $u_0 \leq u_1 < 6$; $\mathscr A(0)$ est donc vraie.
Supposons, pour un entier $n$ quelconque fixé, que $\mathcal A(n)$ soit vraie. Alors \[\begin{aligned} u_n &\leq u_{n+1} < 6& \\ \implies 0,7 u_n &\leq 0,7u_{n+1} < 0,7\times 6& \\ \implies 0,7u_n + 1,8 &\leq 0,7u_{n+1}+1,8 < 4,2 + 1,8& \\ \implies u_{n+1} &\leq u_{n+2} < 6.& \end{aligned}\] Donc $\mathscr A(n+1)$ est alors aussi vraie.
Initialisée et héréditaire, $\mathscr A(n)$ est donc vraie par récurrence pour tout entier naturel $n$.

3.b. Nous venons de démontrer que $(u_n)$ est croissante mais majorée par 6. Cette suite est donc convergente.

3.c. La fonction $x\mapsto 0,7x + 1,8$ étant continue sur $\mathbb R$, la limite $\ell$ vérifie la relation: \[\ell = 0,7\ell + 1,8 \iff 0,3\ell = 1,8 \iff \ell = \frac{1,8}{0,3} =6.\] À long terme, la quantité de médicament dans le sang va se stabiliser autours de 6 mg.

4.a. Pour tout entier naturel $n$: \[\begin{aligned} v_{n+1} &= 6-u_{n+1}& \\ &= 6 - (0,7u_n + 1,8)& \\ &=6 - 0,7u_n - 1,8& \\ &=4,2 - 0,7u_n.& \end{aligned}\] D'autre part, \[v_n = 6 - u_n \iff u_n = 6 - v_n.\] Donc: \[\begin{aligned} v_{n+1} &= 4,2 - 0,7u_n& \\ &= 4,2 - 0,7(6 - v_n)& \\ &= 4,2 - 4,2 + 0,7v_n& \\ &= 0,7v_n.& \end{aligned}\] Donc $(v_n)$ est géométrique de raison $q=0,7$ et de premier terme \[v_0 = 6 - u_0 = 6-2 = 4.\]

4.b. On en déduit que pour tout entier naturel $n$: \[v_n = q^n v_0 = 0,7^n \times 4.\] Donc: \[u_n = 6 - v_n = 6 - 4\times 0,7^n.\]

4.c. On cherche la plus petite valeur de $n$ pour laquelle \begin{align*} &u_n \geq 5,5& \\ \iff &6 - 4\times 0,7^n \geq 5,5& \\ \iff &-4\times 0,7^n \geq 5,5 - 6& \\ \iff &-4\times 0,7^n \geq -0,5& \\ \iff &0,7^n \leq \frac{-0,5}{-4}& \\ \iff &0,7^n \leq 0,125.& \end{align*} Méthode 1. Par essais successifs à l'aide de la calculatrice, on obtient que $0,7^5\approx 0,168$ et $0,7^6\approx 0,1176$.
Donc le traitement devra être arrêté au bout de 6 heures (7 injections).
Méthode 2. \begin{align*} 0,7^n &\leq 0,125& \\ \iff &\ln(0,7^n) \leq \ln(0,125)& \\ \iff &n\ln(0,7) \leq \ln(0,125)& \\ \iff &n \geq \frac{\ln(0,125)}{\ln(0,7)}.& \end{align*} Sachant que $\dfrac{\ln(0,125)}{\ln(0,7)}\approx 5,83$, le plus petit entier qui vérifie cette condition est $n=6$. Il faudra donc traiter le patient pendant 6 heures, donc réaliser 7 injections.

retour

code : 206