AP02-07

retour

1.a. \[\begin{aligned} f'(x) &= 2 \times 3x^2 + 3 \times 2x - 36& \\ &= 6x^2 +6x -36& \\ &= 6(x^2 + 2x - 6).& \end{aligned}\] Donc $f'(x)$ est du signe de $x^2 + 2x - 6$ qui est un polynôme de degré 2.
Son discriminant est : \[ \Delta = 1^2 - 4 \times 1 \times (-6) = 25.\] Ce discriminant est positif, donc le polynôme admet deux racines : \[\begin{aligned} x_1 &= \frac{-1-\sqrt{25}}{2\times 1} = \frac{-1-5}{2}= -3;& \\ x_2 &=\frac{-1 +\sqrt{25}}{2\times 1} = \frac{-1+5} 2 = 2.& \end{aligned}\] Le coefficient de degré 2 est 1, positif, donc $f'(x)$ est positive à l'extérieur des racines.
On peut donc établir le tableau de variations suivant.

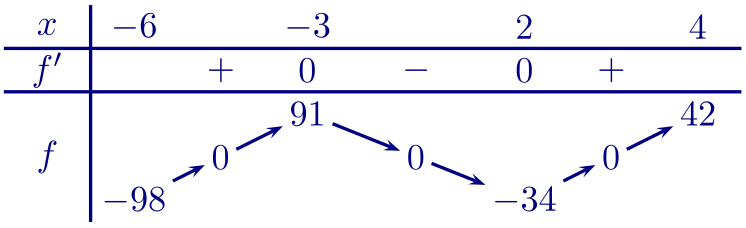
1.b. D'après le tableau de variation, l'équation $f(x)=0$ admet donc 3 solutions.

1.c. À l'aide de la calculatrice, on détermine que ces solutions ont pour valeurs approchées $-5,17$, $0,29$ et $3,38$.

2. La fonction $f$ est dérivable sur $[10;50]$ et pour tout $x$ de cet intervalle : \[f'(x) = 3x^2 - 60x + 302.\] Le discriminant de ce polynôme de degré 2 est : \[\Delta = (-60)^2 - 4 \times 3 \times 302 = -24.\] Ce discriminant étant négatif, il n'y a pas de racine et le polynôme est toujours du signe de son coefficient de degré 2, donc strictement positif.
La fonction $f$ est donc continue et strictement croissante sur $[10;50]$.
De plus $f(10) = 1220$ donc $f(10) < 2000$ tandis que $f(50) = 65300$ donc $f(50) > 2000$.
L'équation $f(x)=2000$ admet donc une unique solution dans $[0;50]$.
Une recherche à la calculatrice permet de préciser que cette solution est voisine de $19,13$.

retour

code : 145