Corrigé du 153 P. 86
retour
1. Pour tout $m\in\mathbb R$: \[\begin{aligned} &(2m^2 + 2)\overrightarrow{AM_m} + 3m\overrightarrow{BM_m} -3m\overrightarrow{CM_m} =\vec 0&\\ \iff& (2m^2+2)\overrightarrow{AM_m} = -3m\overrightarrow{BM_m} + 3m\overrightarrow{CM_m}& \end{aligned}\] Or: \[m^2 \ge 0 \implies 2m^2+2\ge 2 \implies 2m^2+2 \neq 0.\] Donc on peut écrire que : \[\begin{aligned} &(2m^2+2)\overrightarrow{AM_m} = -3m\overrightarrow{BM_m} + 3m\overrightarrow{CM_m}&\\ \implies& \overrightarrow{AM_m} = -\frac{3m}{2m^2+2}\overrightarrow{BM} +\frac{3m}{2m^2+2}\overrightarrow{CM}& \end{aligned}\] Donc $\overrightarrow{AM_m}$ est une combinaison linéaire des vecteurs $\overrightarrow{BM_m}$ et $\overrightarrow{CM_m}$ ce qui signifie que ces vecteurs sont bien coplanaires et donc que les points $A$, $B$, $C$ et $M_m$ le sont aussi.
2.a. Reprenons la relation précédente: \begin{align*} \overrightarrow{AM_m} &=-\frac{3m}{2m^2+2}\overrightarrow{BM} +\frac{3m}{2m^2+2}\overrightarrow{CM}& \\ &=\frac{3m}{2m^2+2}\overrightarrow{MB} +\frac{3m}{2m^2+2}\overrightarrow{CM}& \\ &=\frac{3m}{2m^2+2}\left(\overrightarrow{CM}+\overrightarrow{MB}\right)& \\ &=\frac{3m}{2m^2+2}\overrightarrow{CB}.& \end{align*}
2.b. Donc $M_m$ se situe sur la droite parallèle à $(CB)$ passant par $A$, c'est à dire la droite $(AD)$.
3.
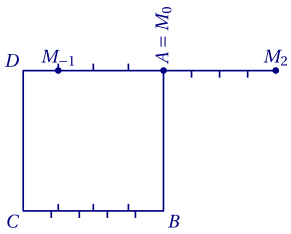
Si $m = 0$,
$\overrightarrow{AM_0} = \dfrac{3\times 0}{2\times 0^2+2}\overrightarrow{CB}=\vec 0$.
Si $m=2$,
$\overrightarrow{AM_2} = \dfrac{3\times 2}{2\times 2^2+2}\overrightarrow{CB}
=\dfrac 4 5 \overrightarrow{CB}$.
Si $m = -1$,
$\overrightarrow{AM_{-1}} = \dfrac{3\times (-1)}{2\times (-1)^2+2}
\overrightarrow{CB}
=-\dfrac{3}4\overrightarrow{CB}
=\dfrac 3 4 \overrightarrow{BC}$.
D'où la figure ci-dessous.
4.a. On a montré à la question 1 que le dénominateur de cette fraction ne s'annule pas. $f$ est donc bien définie sur $\mathbb R$.
4.b. Pour tout réel $x$ non nul. \[f(x) = \frac{3x}{2x^2+2} =\frac{x}{x^2} \times \frac{3}{2 + \frac 2 {x^2}} =\frac 1 x \times \frac{3}{2+\frac 2 {x^2}}. \] Or: \[\lim_{x\to\pm\infty} \frac 2 {x^2} = 0 \implies \lim_{x\to\pm\infty}\frac{3}{2+\frac 2 {x^2}} =\frac{3}{2+0} =\frac 3 2.\] D'autre part: \[\lim_{x\to\pm\infty} \frac 1 x = 0.\] Donc: \[\lim_{x\to\pm\infty}\frac 1 x \times \frac{3}{2+\frac 2{x^2}} = 0 \times \frac 3 2 = 0.\]
4.c.
$f$ est dérivable sur $\mathbb R$ et pour tout réel $x$:
\[\begin{aligned}
f'(x) &=
\frac{3(2x^2+2) - (3x)(4x)}{(2x^2+2)^2}&
\\
&=\frac{6x^2 + 6 - 12x^2}{(2x^2+2)^2}&
\\
&=\frac{-6x^2 + 6}{(2x^2+2)^2}&
\end{aligned}\]
Le dénominateur étant strictement positif, $f'(x)$ est du même signe que $-6x^2 + 6$.
C'est un polynôme de degré 2 dont les racines évidentes sont $-1$ et $1$.
De plus, son coefficient principal, $-6$, est négatif. Donc on peut établir le tableau de variation suivant.
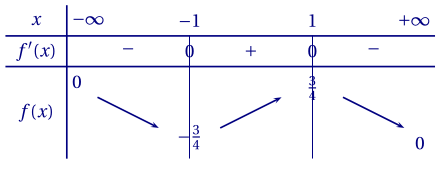
5.a. D'après le tableau de variation: \[\begin{aligned} \forall x\in\mathbb R\quad &f(x) \in \left[-\frac 3 4;\frac 3 4\right]& \\ \iff \forall m\in\mathbb R\quad &\frac{3m}{2m^2+2} \in \left[-\frac 3 4;\frac 3 4\right].& \end{aligned}\]
5.b. Non, car on vient de montrer que $\dfrac{3m}{2m^2+2}$ ne prend pas toutes les valeurs réelles.
5.c.
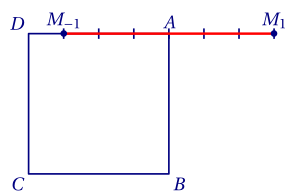
On a
\[\overrightarrow{AM_1}=\frac 3 4 \overrightarrow{CB}.\]
Puisque $\dfrac{3m}{2m^2+2}$ décrit l'intervalle $\left[-\dfrac 3 4;\dfrac 3 4\right]$, $M_m$ parcours le segment $[M_{-1};M_1]$.
retour