Corrigé du 152 P. 86
retour
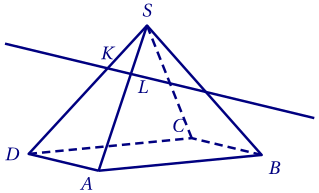
1.
Les points $O$, $B$, $C$ et $S$ étant les sommets d'un tétraèdre, ils ne sont
donc pas coplanaires.
Par conséquent, les vecteurs $\overrightarrow{OB}$, $\overrightarrow{OC}$ et $\overrightarrow{OS}$ ne le sont pas non plus,
et $(O;\overrightarrow{OB},\overrightarrow{OC},\overrightarrow{OS})$ est bien un repère de l'espace.
2.a. Déterminons les coordonnées de $K$: \begin{align*} \overrightarrow{SK} &= \frac 1 3 \overrightarrow{SD}& \\ \implies \overrightarrow{SO}+\overrightarrow{OK}&=\frac 1 3 \left(\overrightarrow{SO}+\overrightarrow{OD}\right)& \\ \implies \overrightarrow{OK} &= \frac 1 3 \overrightarrow{SO}-\overrightarrow{SO}+\frac 1 3\overrightarrow{OD}& \\ \implies \overrightarrow{OK}&= \frac 2 3 \overrightarrow{OS} + \frac 1 3 \overrightarrow{OD}& \\ \implies &K\begin{pmatrix}-\frac 1 3\\0\\ \frac 2 3\end{pmatrix}.& \end{align*}
2.b. $I$ est le milieu de $[SO]$ donc \[\overrightarrow{OI}=\frac 1 2\overrightarrow{OS} \implies I\begin{pmatrix} 0 \\ 0 \\ \frac 1 2\end{pmatrix}.\] Alors $\overrightarrow{BI}$ a pour coordonnées \[\begin{pmatrix}0 - 1\\0 - 0\\ \frac 1 2 - 0 \end{pmatrix} =\begin{pmatrix}-1\\ 0 \\ \frac 1 2\end{pmatrix}.\] De même, $\overrightarrow{BK}$ a pour coordonnées: \[\begin{pmatrix}-\frac 1 3 - 1\\ 0 - 0 \\ \frac 2 3 - 0 \end{pmatrix} = \begin{pmatrix}-\frac 4 3\\ 0 \\ \frac 2 3\end{pmatrix}. \] $B$, $K$ et $I$ seront alignés si et seulement si $\overrightarrow{BK}$ et $\overrightarrow{BI}$ sont colinéaires, donc si et seulement si on peut trouver un réel $\alpha$ tel que: \[\begin{aligned} &\overrightarrow{BK}=\alpha\overrightarrow{BI}& \\ \iff &\begin{cases} -\frac 4 3 = -\alpha\\ 0 = 0\\ \frac 2 3 = \frac 1 2 \alpha \end{cases}& \\ \iff &\begin{cases} \alpha = \frac 4 3\\ \alpha = \frac 2 3 \times 2 = \frac 4 3 \end{cases}& \\ \iff &\alpha = \frac 4 3.& \end{aligned}\] Donc les points $B$, $I$ et $K$ sont alignés.
3.
Puisque $B$, $I$ et $K$ sont alignés, $K$ est sur la droite $(BI)$, elle-même incluse dans le plan $(BCI)$.
Il appartient donc à $(BCI)$.
De même, par construction, $L$ est sur $(BCI)$.
Donc la droite $(KL)$ entière appartient au plan $(BCI)$.
D'autre part, puisque $L$ est sur $[SA]$, $L$ appartient au plan $(SAD)$.
La relation $\overrightarrow{SK} = \dfrac 1 3 \overrightarrow{SD}$ nous apprend que $K$ appartient à la droite $(SD)$,
incluse dans le plan $(SAD)$, donc $L$ appartient au plan $(SAD)$.
La droite $(KL)$ appartient à la fois au plan $(BCI)$ et au plan $(SAD)$, or ces plans se coupent selon une unique droite,
donc $(KL)$ est bien la droite d'intersection de ces deux plans.
4.
Raisonnons par l'absurde en supposant que $(KL)$ et $(AD)$ ne sont pas parallèles.
Alors les vecteurs $\overrightarrow{KL}$ et $\overrightarrow{AD}$ ne sont pas colinéaires et forment donc une base du plan $(SAD)$.
Mais $\overrightarrow{BC}=\overrightarrow{AD}$, donc $\overrightarrow{KL}$ et $\overrightarrow{BC}$ ne sont pas colinéaires non plus
et forment donc une base du plan $(BCI)$.
$\left(\overrightarrow{DA},\overrightarrow{KL}\right)$ est donc une base à la fois des plans $(SAD)$ et $(BCI)$.
Cela implique que ces plans sont parallèles, ce qui est absurde car ils sont sécants selon $(KL)$.
Donc notre hypothèse de départ est fausse, et les droites $(KL)$ et $(AD)$ sont bien parallèles.
5. Puisque $(KL)$ est parallèle à $(AD)$, et que $\overrightarrow{SK}=\frac 1 3 \overrightarrow{SD}$, le théorème de Thalès permet d'affirmer que \[\begin{aligned} &\overrightarrow{SL} = \frac 1 3 \overrightarrow{SA}& \\ \implies &\overrightarrow{SO}+\overrightarrow{OL} =\frac 1 3 \overrightarrow{SO}+ \frac 1 3 \overrightarrow{OA}& \\ \implies &\overrightarrow{OL} = \frac 2 3 \overrightarrow{OS} +\frac 1 3 \overrightarrow{OC}& \\ \implies &L\begin{pmatrix}0 \\ \frac 1 3 \\ \frac 2 3\end{pmatrix}& \end{aligned}\]
retour