Corrigé du 145 P. 84

retour

1. Voir ci-dessous.
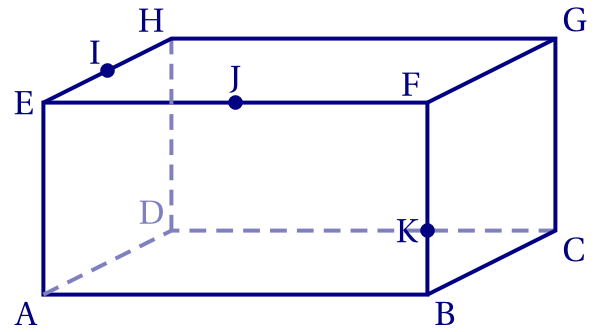
figure

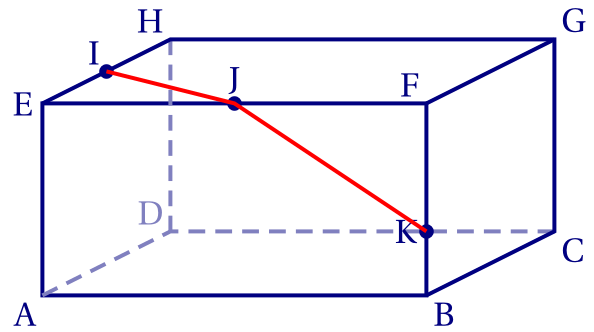
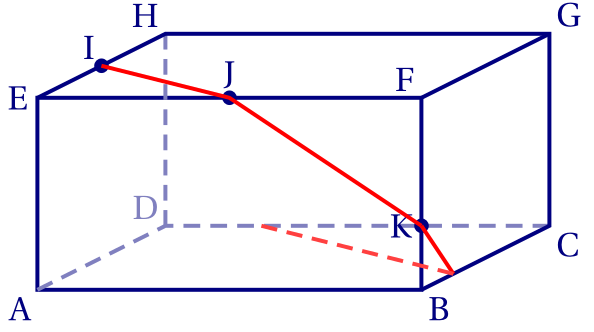
2. Les points I et J sont à la fois sur le plan (IJK) et sur la face EFGH. L'intersection du plan (IJK) avec cette face est donc le segment [IJ].
De même, les points J et K sont à la fois sur le plan (IJK) et sur la face ABFE. L'intersection de ce plan avec cette face est donc le segment [JK].
figure

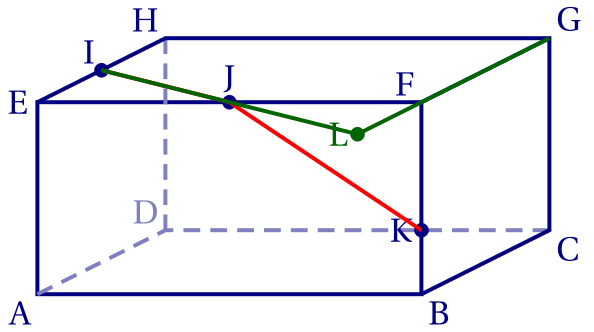
3.a. La droite (IJ) n'est pas parallèle à la droite (FG) (car sinon, I appartenant à (EH) qui est parallèle à (FG), J devrait aussi lui appartenir).
Les droites (IJ) et (FG) sont cependant coplanaires, car toutes deux dans le plan (EFG).
Ces droites sont donc nécessairement sécantes.
figure

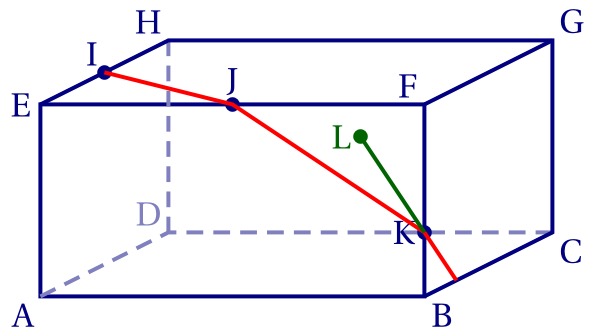
3.b. Puisque L appartient à la droite (IJ), il appartient au plan (IJK). Puisque L est sur (FG), il appartient aussi au plan contenant la face FGCB.
Le point K appartient également à ces deux plans qui se coupent selon la droite (LK). La partie de (LK) à l'intérieur de FGCB est donc l'intersection recherchée.
figure

4. Les plans (ABC) et (EFG) sont parallèles. Le plan (IJK) les coupe donc selon des droites parallèles. Le plan (IJK) coupe donc la face ABCD selon une droite parallèle à (IJ).
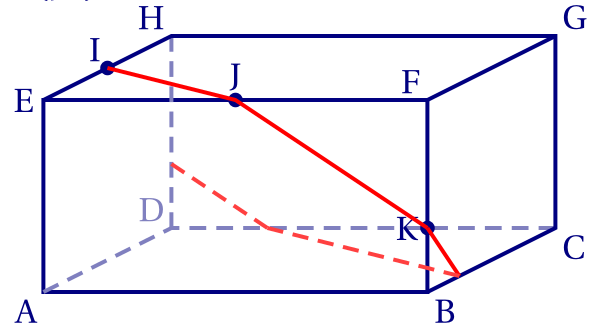
figure

5. Les plans (ABF) et (DCG) étant parallèles, le plan (IJK) les coupe selon des droites parallèles. L'intersection de (IJK) avec la face DCGH est donc parallèle à (JK).
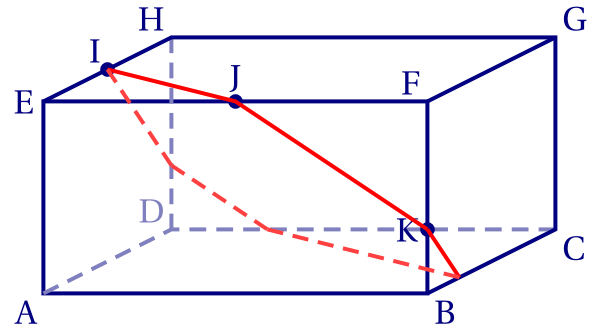
figure

Il ne reste plus qu'à tracer la section de la face ADHE.
figure

retour